ＣＳ四方山話（第25話）暗号を理解するための数学の世界その4
小学生からの数学シリーズ・第四弾「10進数の話（＋16進数の話）」

今回は「小学校からの数学」シリーズ・四弾です。前回の第三弾（ＣＳ四方山話 第24話）での予告通り、「10進数」の話（＋16進数の話）です。（旧基準）小学１年生でも学ぶ10進数での「繰り上がり・繰り下がり」に話を進めます。

ｎ進数の呼称についての秘密

前回（第24話で）登場した１進数、２進数を含め、日本語では「○○進数」という表現で（捻りがなく、味気ない気もしますが）分かり易いです。

英語では、下記のようになります。

　unary number        １進数
　binary number       ２進数
　decimal number    10進数、小数
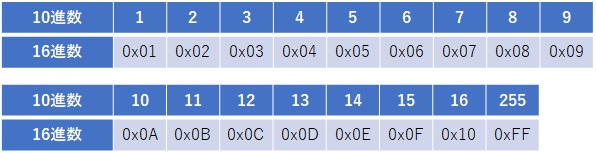
　hexadecimal          16進数

unary は「単項」という意味です。unary operator は（プログラミングをするヒトは良く知っている）「単項演算子」のことです。

binary は、ラテン語の binarius =「２つから成る」が語源です。binary file という言い方をしますが、これは人間が読める文字（text）ではなく、コンピュータが読める２進数表記で書かれたファイルということになります。

deci は decimus  = 1/10 というラテン語が語源です。deca は 10 というギリシャ語です。化学の数に関する接頭語は、ラテン語だとｎ倍、ギリシャ語だと 1/n 倍というルールになっています。

デシリットル は 1/10 リットル ということになります。decimal には小数という意味もあります。

hexadeci は 1/16 という意味で、hexadecimal は number が付かない単体で 16進数 という意味になります。なぜ number が付かなくなるのかは分かりません。

ちなみに……　ニュースや仕事の場面でも盛んに登場する「デジタル」= digital の語源は ラテン語 の digitus = 指で、それが変化して digitalis になり、15世紀に 英語化して digital になりました。

10進数（deci-mal）ではなく、binary じゃないの？と思うかも知れませんが、アナログコンピュータ = analog computer との対比で、数えられる数値で処理を行う計算機ということで digital computer と呼ばれるようになりました。

10進数（decimal number）について

なぜ、ヒトは日常的に８進数や12進数ではなく、10進数を使うようになったのか？　それは、ヒトの身体的特徴に依るものでしょう。
　
ヒトの手指は（足指もですが）両手の合計で10本あります。ですので「10」、ひとまとまりにして考えるようになり、10よりも小さい数に記号を付けたということになるのでしょう。

我々が日常的に使っているのは「アラビア数字」ですが、これ以外に「ローマ数字」があります。ローマ数字では、次のようになります。

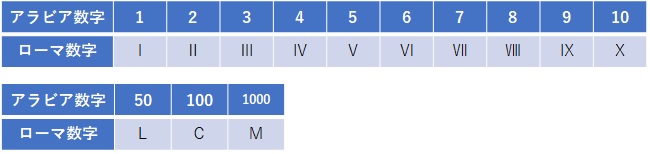
たとえば、2023 は MMXXⅢ となります。10だけでなく、片手の指も数の「5」も基準になっていることが分かります。３までは１進数的な表現ですが、次が５に１足りない「４」という表現になっているのが面白いです。減算を含む加法によって数を表現しているということになります。

繰り上がり／繰り下がりについて

さて、いよいよ、繰り上がり／繰り下がりです。

２進数の場合と同じように、０を含む10個の数を表す記号を使い切ったら、左側に枠を１つ増やすという方法で表現します。

演算としては２進数の場合よりは少し複雑になります。10の塊を意識して計算する必要があります。６＋７は、６に４を足せば10になるので、7から4を借りて10にして、７から４を取った残りが３になるので「１３」ということになります。これが繰り上がりです。

　６＋８＝６＋（４＋３）＝（６＋４）＋３＝10＋３＝13

減算の場合も10の塊を意識します。３は７よりも小さいので、３と10に分けて、10から７を引いておいて、分けた残りを足すということになります。これが繰り下がりです。

　13 – 7 = ( 3 + 10 ) – 7 = 3 +  ( 10 – 7 ) = 3 + 3 = ６

この説明で小学１年生に伝わらない場合は、「数え棒」を使って解説必要がありますが、皆さんにはこれで充分でしょう。

数え棒よりは、日本人には算盤（そろばん）の方が分かり易いのかも知れません。ここでも、ローマ数字と同様に「５」と「10」が登場します。

何進数でも考えることは可能です。ただ、ｎ進数のｎが多くなると、大きな数字をよりコンパクトに表現できますが、数値を定義する記号の数は増えます。ヒトの手指の数が10だったこともあり、０を含む10個の数を表す記号で表現するのが実用上ちょうどバランスが良かったので、ヒトは10進数を使うようになったのでしょう（筆者の勝手な推測ですが……）。

12進数について

数学的には12進数を使うことはありませんが、日常生活では12を１つの塊とする考え方があります。12は使い勝手の良い数値で、２，３，４，６のいずれにも分けられます。古代メソポタミアでは12進数を使っており、その影響は現在の世界にも残っています。

英語には dozen という単位があります。語源は、ラテン語の「duodecim」= 12 です。日本でも１箱の中のチョコレートの数が12だったり、ビールの１ケースが12本入りだったりします。また、１年は12ヶ月ですし、半日は12時間ですし、１時間は 12 x 5 = 60分です。 国際単位系であるＳＩに統一される方向ですが、英語圏ではいまだに「ヤード・ポンド法」も用いられています。長さの単位である、１feet は 12inch です。タイヤのサイズや、ディスプレイの大きさは、日本においてもインチで表現されます（なぜだか分かりませんが、きっと何かしら歴史的な経緯があるのでしょう）。

16進数について

デジタルコンピュータとしては、基本は２進数なので、「２のべき乗」、2^n が都合が良いです。8進数 だと「8」「9」が出て来ない。使わない記号があって、もったいない。かつ 2^3 で（偶数乗じゃない = 何かの２乗ではない）ので綺麗じゃない。32進数は文字数が増えすぎる、かつ2^5 で綺麗じゃない。

ということで、2^4 = 16 進数という表現を使うようになったのだと思います。足りない記号はアルファベットを使えば良いということで、デジタルコンピュータの界隈では16進数がよく出て来ます。

まとめ

ｎ進数 の説明で長くなりましたが、今回（第25話）で、ようやく「小学１年生の数学」は終了です。新基準自然数の加法（加算、減算）と、その時の繰り上がり／繰り下がりとを学びました。次回（第26話）からは「小学２年生の数学」になります。

---

四方山話

「小学校からの数学」シリーズは、なかなかの大物で文字数（話数）を喰っています。このペースで暗号まで到達するには時間が掛かりそうですが、こうして体系立てて「数」というモノを学んでいけば「数学」も身近なものになって、コンピュータや暗号と親しくなれるのでは？　と思っていますので、ゆっくりお付き合い頂ければ幸いです。

ということで、ＣＳ = CyberSecurity から少し遠ざかっていますので、今回はこの枠の「四方山話」でＣＳの小ネタ扱ってみます。

一般の方でも「脆弱性（ぜいじゃくせい）」という言葉を聞く機会が増えていると思います。その  脆弱性とは、コンピュータのOSやソフトウェアにおいて、プログラムの不具合や設計ミスが原因となって発生した情報セキュリティ上の欠陥のことを言います。脆弱性は「セキュリティホール」とも呼ばれます。脆弱性が残された状態でコンピュータを利用していると、不正アクセスに利用されたり、ウイルスに感染したりする危険性があります。塞がなければいけない「穴」ということです。

Windows、MacOS、Linux などのＯＳ（オペレーションシステム）や、ブラウザや表計算ソフトなどのアプリケーションは、かなり大規模なプログラムですので「完璧」にはなり得ません。複数の欠陥、つまり脆弱性が潜んでおり、それが発見されていくことになります。また、機能向上などによって新たに書かれるプログラムでは、新たな脆弱性が作り込まれる場合もあります。

自分の環境（個人であればPCやルータなど、オフィスであればサーバーやNASなどにも）に潜んでいる脆弱性を確認し、対策を打つことが大切です。

直近、どのようなペースで脆弱性が報告されているのかを調べてみました。

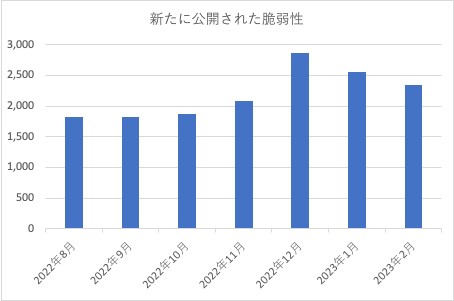
毎月2000件前後の脆弱性が発見＆公開されています。

こうして新たな脆弱性が登場するので、脆弱性の確認は定期的に行う必要があります。また、設定の不備によって脆弱性が作り込まれることもあります。設定変更は慎重に行うことが必要ですが、「ヒトはミスをする」ことを前提に考える必要があります。その観点でも、脆弱性の確認を定期的に行うことが望まれます。

---

ＣＳ四方山話の過去の記事はこちら（合わせてお読みください）

サイバーセキュリティ四方山話の最新話は、メールマガジンにてもご案内致しています。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。