ＣＳ四方山話（第28話）　暗号を理解するための数学の世界その7

小学校からの数学シリーズ・第7弾

「小学校からの数学」シリーズ・第7弾です。前回の第6弾（ＣＳ四方山話 第27話）の続き「小学２年生」です。少し間が空きましたが、サボっていた訳ではありません。ヒトの成長とは、なかなか線形には進まないということの象徴だと思ってください（←完全に言い逃れですが (^^;;）。

小学２年生で学ぶ基本的な単位を覚えていますか？

小学２年生の課程には「単位」が登場します。まず１つ目は「長さ」です。m、cm、mm。

ヒトにとって、使い易い単位は cm でしょう。その辺にあるモノは 数cm から 10数cm、数10cm のモノが多いでしょう。自分自身の大きさも、例えば 170cm ですから、身近なモノは cm で表現すると、１桁から３桁のごく前半で表現することが可能です。ということで、なじみ深い cm をまず学びます。

長さを cm（センチメートル）で表現すること（単位としての cm を理解すること）、ものさしを使って長さを計ってみること（身近なものを cm で表現すること）、ものさしを使って指定された長さの線分を描くこと、この３つを学ぶことになります。

いろいろな単位がありますが、「メートル法」という言葉があるように「長さ」が単位の基本です。「メートル法」をブラシアップしたものが「ＳＩ（国際単位系）」で、地球では３ヵ国を除くすべての国が採用しています。

メートル（ｍ）は、皆さんもご存知の通り、地球の北極点から赤道までの子午線弧長の「1000万分の1」として定義され、現在はより精度を高めるために「1/299792458 分の1秒間に光が真空中を伝わる長さ」として定義されています。論理的な順番としては「ｍ」から学習するべきなのですが、身近なモノ（計りやすいモノ）ということで、cm → mm → m という順番で学習するようです。

小学２年生で登場する２つ目は「体積（容積）」です（小学２年生の教科書では「かさ」と表記するのが一般的なようです）。

L（リットル）、dL（デシリットル）、mL（ミリリットル）です。昔は、ℓ、dℓ、mℓと表記していましたが、現在では、この筆記体の「ℓ」は用いず、大文字「L」に統一されたようです。「L」は、SI単位ではありませんが「SIと併用される単位」とされています。1L = 10^－3 m^3 です。

個人的な感想になりますが、（身近な）容積としては「L」「cc」が多いように思います。「cc」とは何ですか？　と聞くと回答を得られない場合が意外と多いのですが、cc = cubic centimetre = 立方センチメートルの意味で、1cc = 10^－6 m^3 です。1mL = 10^－3 L = 10^－6 m^3 なので、1cc = 1mL です。

前述の通り「L」はSIの補助単位ですが、「cc」は「mL」の補助単位と定められています。「手下の手下」という位置付けなので、「cc」は推奨されておらず、いろいろな製品の表記は「mL」に統一されていくようです。

単位と圏論との関係、さらに単位系を変換する関手とは？

単位の話が主体になると「数学」との接点が難しくなりますので、単位と圏論を結び付けてみましょう。小学２年生の範囲からは逸脱しますが、ご容赦ください。

単位系としては、SI（国際単位系）、CGS単位系（cm, g, sec.）、ヤードポンド法（yd：ヤード、lb：ポンド、℉：華氏）、幾何学単位系（c：光速、G：万有引力定数）、プランク単位系（c、G、ディラック定数、クーロン力定数、ボルツマン定数）などなど、さまざまなモノがあります。

さて本題です。

圏論の「圏」(category) とは、「対象」 (object)と「射」 (arrow) で記述されるモノです。単位系は、前述の通り、複数存在します。そして、ある単位系の単位を、別の単位系の単位に変換することが可能です。この変換は「関数 」(function)ということになります。ある単位系自体を別の単位系に変換することも可能で、この変換は「関手」(functor)と呼ばれます。

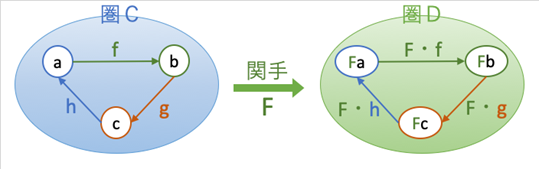
構造を保ったまま、別のテーマに応用（マッピング）できる。あるドメインに適用したプログラムを、別のドメインに適用できるように変換できること。これらは「関手」の概念です。 「関手」は、プログラムを書くヒト = programmer にとっては、言葉は知っていなかったとしても「日常」でしょう（逆に言えば、それが日常でなければ、その概念を把握できないので、programming を仕事にするのは止めた方が良いでしょう）。

Programmer ではない方々に「関手」のイメージをお伝えするとしたら、よく話題に上がる「ビジネスの横展開」は「関手」と言えるでしょう。ただし（真っ当な）program のようにいつも「関手」が成立するとは限らない、という点には留意が必要でしょう。「関手」が成立するためには、「恒等射の保存」と「合成の保存」が条件となります。これを知っていると、自分が描いたビジネスの横展開が整理するかどうかを検証することも可能では？　だと思います（知らんけど……）。Programmer だけでなく、みんな圏論を学びましょう！

まとめ

さて今回（第28話）で、ようやく小学２年生の課程が終了です。実際に小学２年生で圏論を学ぶわけではありません。ただ小学２年生で学ぶ事柄にも圏論に繋がる概念があることを理解してもらえれば幸いです。数学は、あらゆる場面に登場するということです。次回（第29話）は、小学３年生に進級します。

---

四方山話

単位系の中で「タチが悪い」のは、ヤードポンド法です。

SIを採用していない国が３ヵ国あると述べましたが、それは米国、ミャンマー、リベリアです。米国が弱小国であれば良いのですが、そうではない点が話をややこしくしています（米国政府としてはメートル法を推奨していますが、米国は自由の国なので強制はしません。その結果、SI統一は画竜点睛を欠く状態となっています）。

SI では 温度の単位は「K」（ケルビン、絶対温度、熱力学温度）で、SI組立単位として「℃」が定義されています。ヤードポンド法では温度も「℉」で悉く相容れませんね。

単位系の話は、歴史や文化にも関係するので一筋縄では行きません。

私自身も、車の排気量を「2400mL」で表現されてもピンときません。ガソリンエンジン車がなくなれば排気量という概念もなくなりますが、完全EV化も簡単には進まないようなので、まだそうなるには時間が掛かるでしょう。また、タイヤ・ホイールも「インチ」ですよね。ネジもインチねじがなくなり、ミリねじだけになるという整理は急速には進まないでしょう。 先にできてしまった規格や標準は、その出来が悪くても普及してしまったもの勝ちなのです。その最たるものが Internet Protocol で、それ故に我々は Cyber Security を考えざるを得ないということなのです。飯の種になっているから良いのでは？　と言う見方もできますが、やはり世界はもっと綺麗であるべきとも思う次第です。

---

ＣＳ四方山話の過去の記事はこちら（合わせてお読みください）

サイバーセキュリティ四方山話の最新話は、メールマガジンにてもご案内致しています。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。