ＣＳ白狐村塾（第２話）楕円曲線暗号について

はじめに

「ＣＳ四方山話・第11話」が２月１日に公開され、読んでくださった方々かコメントを頂いたりしています。そうした反応は、読んで頂いているという実感が湧き、本当に励みになります。

「専門用語に格闘しながらも、楽しく拝見させていただきました。身近なところでのセキュリティ対策の参考にさせていただけることが幾つもありました。ありがとうございました」という有り難いお言葉を頂き、「四方山話」は「より分かり易く」を心掛けねばと思っています。

そのカウンタということでもありませんが「白狐村塾」は、もう少し深く、でも、分かり易くを目指せればと考えています（自分で、ハードルを上げている気もしますが……）。

前回は、暗号化方式の中でも広く使われているRSA暗号を取り上げました。今回は（予告通り）、適用される場面が増えている、楕円曲線暗号について、お話しさせていただきます。

楕円曲線？ 楕円？ 楕円と暗号の関係性

何が「楕円」？ 楕円と暗号がどう関わるのか？ まずは、そこからですね。

楕円は、皆さんもご存知の通り、長軸と短軸を持つ円を少し潰したような形状の図形です。ただ、この「楕円」と「楕円曲線」とは、あまり関係はありません。楕円を扱う関数は、円を扱う関数（三角関数など）をもう少し複雑にしたものになる、と言った辺りの研究の流れの中で「楕円曲線」と呼ばれるようになった、と理解すれば良いのでは？ と思います (※1)。

楕円曲線を正しく理解するためには、「群・環・体」という代数学の「基本」を理解する必要があります。どんどん、得たいの知れない言葉が出てきて「？」が増える一方ですよね。それは分かりつつ、無理を承知で「数学」全体の中での「楕円曲線」を説明してみます。一旦、区切りを付けないと先に進めないので。

群・環・体

「代数学」とは「数学」全体の骨組みを考える学問です。そして、その代数学の「基本」が「群・環・体」です。ちなみに、私は、大学の時にそんな名前の教科書があったよなぁ……ぐらいの記憶でした。代数学に関しては基礎すら理解していなかったということになります。基本的に「整数」の世界で動作するコンピュータを生業にするようになってから、再履修したようなものです。

「群・環・体」は、それぞれ（値の）集合と演算がセットになったものです。

その中で「群」の定義は、次の通りです。集合をＧとします（Gun だから G なのではなく、群 = Group なので G です）。（二項）演算を🔺と定義します。

1)　集合Ｇに含まれる ある要素 e と任意の要素 g に関して、下記が成り立つ
e🔺g=g🔺e=g
　2)　集合Ｇに含まれる ある要素 h と任意の要素 g に関して、下記が成り立つ
h🔺g=g🔺h=e
　3)　演算🔺に関して、常に結合法則が成り立つ
結合法則とは、下記が成り立つことです（これは私でも知っていました）。
(a🔺b)🔺c =a🔺(b🔺c)
　さらに、下記の条件も充足する場合、群 (Ｇ, 🔺) は「可換群（アルベール群）」と呼ばれます。
　4) 演算🔺に関して、常に交換法則が成り立つ
交換法則とは、下記が成り立つことです（これも私でも分かります！）。
a🔺b =b🔺a

定義だけでは分かり難いので、具体例を考えてみましょう。
Ｇ は 整数の集合、演算🔺は（通常の）加法（足し算）だとします。
先の条件を当てはめてみます。

1)　任意の整数 n に対して、n+0=0+n=n が成り立つ
2)　任意の整数 n に対して、n+ -n= -n+n=0 が成り立つ
3)　任意の整数 n, m, p に対して、(m+n)+p=m+(n+p) が成り立つ
4)　任意の整数 n, m, p に対して、m+n=n+m が成り立つ

故に、( 整数, 加法 ) は 群 であり、可換群（アルベール群）であるということになります。

楕円曲線

さて、次は楕円曲線です。

　その定義に関しては、色々な表現が可能ですが、シンプルに表現すると下記になります。

• 種数 1 の非特異な射影代数曲線、さらに一般的には、特定の基点 O を持つ種数 1 の代数曲線

　「種数」「非特異」、「射影代数曲線」..、謎の言葉の連続でサッパリ分かりません（少なくとも、私には…）。

もう少しイメージしやすい表現として、暗号で用いられる楕円曲線の表現としては、下記になります。

射影空間上で定義された非特異曲線
y²=x³+ax+b
に双有理同値な曲線
ある有限体Ｋ上の式
y²=x³+ax+b
を満たす全ての点P(x,y) の集合に、無限遠点と呼ばれる特別な点Ｏを加えたもの
x と y は有限体Ｋの要素。
ただし、Ｋの標数が2または3の場合、上式では不都合が生じるため、標数は2と3以外であるとする。

「射影空間」「非特異」、「双有理同値」..、先程と似たような言葉は混じりますが、謎の言葉でサッパリ分かりません（少なくとも、私には）。

　この謎の言葉を掘り出すと深みに嵌まっていくことになるので、その特性のみに着目することにします。
　射影空間上の楕円曲線の有理点はアルベール群を成します（やっと、群の話と繋がりました）。
　これが、楕円曲線がもてはやされる（＝深く研究される）理由で、楕円曲線上の有理点には「群」という構造があり、しかも有限生成であるという特徴が重要です。

射影空間というのは「グラフ」だと思ってください。y²=x³+ax+b を グラフで表すと次のようになります。

左辺が普通の「y」の（「２乗」が付かない）場合は、高校の授業で見掛けた方も居られるかも知れません（数Ⅱｂでしたっけ？懐かしいｗ）。

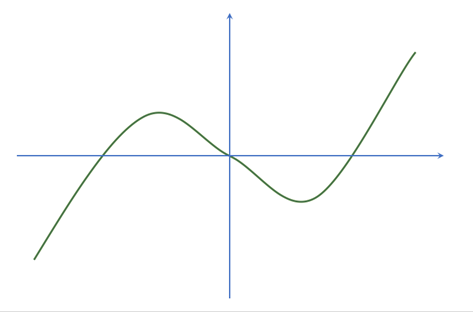
左辺が２乗になっているので、グラフとしては図の実線の部分になります。

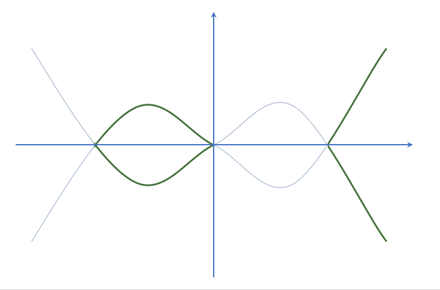
• 楕円離散対数問題

　いいいよ、暗号に関わる特性に関してです。

　暗号は、解けるけど解きにくいという性質によって成立します。現在のコンピュータで実用的な時間で解けなければ「暗号」ということになる訳です。

　前回（白狐村塾・第１話）の「ＲＳＡ暗号」を思い出してください。ＲＳＡ暗号は、大きな素数の積である整数の素因数分解は難しいという特性によって成立しています。

　楕円曲線上での座標（Ｐ，Ｑ）の加法演算（Ｐ＋Ｑ）は、次のように定義されます。

　　　Ｐ＋Ｑ＝Ｒ：楕円曲線上の点Ｐ、Ｑを通る曲線と楕円曲線との交点のｘ軸対象点

　先程のグラフで表現すると、次のようになります。

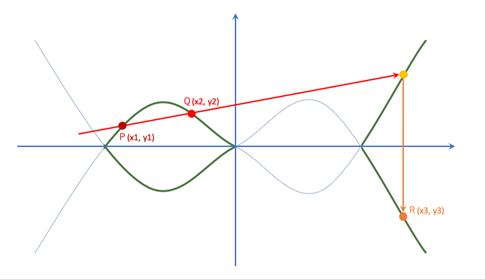
この演算を繰り返します。
R₁=P+Q
R₂=R₂+Q
：
R_n=R_(n+1)+Q
　Ｐ、Ｑ と hash(R_n,p) が分かっていて、n は何でしょう？という問題です（p を標数と呼びます）。

標数p が 256bits の場合、2030年までは安全とされている2048bits のRSA暗号と同程度以上の安全性（＝解きにくさ）を持つことが確認されています (※2)。

　楕円曲線関数の１つである Curve25519 (※3) は、2005年に公開されました、2017年に NIST が SP 800-186 に Curve25519 が追加されることを発表し、米政府によって承認された楕円曲線ということになりました。Curve25519 は 2016年に RFC 7748 (※4) として登録されています。

　Curve25519 を適用しハッシュ関数として SHA-512 を用いた Ed25519 という「エドワーズ曲線デジタル署名」の一種は、OpenSSH の 6.5 以降で採用されるなど普及しています。
　SYNCHRO の KATABAMI というシリーズでもCurve25519を使っており、KATABAMI Chat というセキュア・チャットシステムで事務局さんと原稿のやり取りを行っていますので、この原稿もCurve25519で暗号化されてインターネット経由で伝送されることになります。

まとめ

さて、今回は、楕円曲線暗号に関して説明しました。

　数学はとても優雅で、独創性によって切り拓かれる世界です。数学者であり、物理学者であり、天文学者でもあった天才ヨハン・カール・フリードリヒ・ガウスは「数学は科学の女王であり、数論は数学の女王である」評しています。創造性が勝負の数学の世界は、若い方々が活躍しやすい分野です。たまたまこの記事を読んで下さって、数学って素敵！と思った（精神的に）若い方がおられましたら、数学、特に暗号などにつながる代数学の沼にハマってください。

　ところで、第２話では楕円曲線暗号とストリーム暗号を説明するとかいうことを誰かが言っていましたが、ストリーム暗号に関しては「第３話」の題材となりますので、次回もお楽しみに！

---

(※1) 楕円曲線

　詳しく説明すると教科書一冊になるので、端折って説明します。

1)楕円の孤長を算出する式に関連するということで、y²=f(x) で定義される代数曲線を「楕円関数」と呼ぶことになりました。

　代数学では、代数関数、閉リーマン面、代数曲線の深い関係性を「三位一体」と呼びます。

　「楕円積分」というアルベール積分と同じ「全単射が成立し種数１」という性質を持つリーマン面を「楕円曲線」と呼び、アルベール積分で求められるアルベール関数を「楕円関数」と呼ぶことになったそうです。

　ということで、図形の「楕円」とは無関係ではありませんが「直接の関係はない」ということになります。

(※2) 「公開鍵暗号を巡る新しい動き：RSAから楕円曲線暗号へ」（金融研究 2013.7）
https://www.imes.boj.or.jp/research/papers/japanese/kk32-3-2.pdf

(※3) Curve25519

　この25519という数字は何でしょうか？RFCのようにシリアルナンバでしょうか？残念ながた違います。楕円曲線はそんな膨大な数は提案されていません。

この楕円曲線は、素数 2²⁵⁵-19 におけるモンゴメリ型楕円曲線 y²=x³+486662 x²+x として定義されます。25519は、その素数の係数から来ています。

(※4) RFC 7748
https://datatracker.ietf.org/doc/html/rfc7748

---

白狐村塾話の過去の記事はこちら（合わせてお読みください）
ＣＳ白狐村塾（第１話）サイバーセキュリティに必須の技術、詳細に解説！　その1
ＣＳ白狐村塾（第１話）サイバーセキュリティに必須の技術、詳細に解説！　その2

サイバーセキュリティ白狐村塾は、新たなお話が公開されたときにメールマガジンにてご案内致します。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。