白狐村塾（第4話）
情報システムをリードするために、代数学の基礎を押さえよう！

私は、プログラミングをしたり、システムを設計・構築をしたりする皆さんに代数学の基礎は押さえていて欲しいと思っています。これからのシステムは「通信」を抜きには考えられません。また、通信で連接される複合システムにおいては、セキュリティの観点で「暗号」も欠かすことはできません。そして、通信も暗号も数学、特に代数学が土台になっているからです。

世の中にはさまざまな仕事があるので、誰も彼もが情報システムを生業にする訳ではないと思います。これからの時代、10人に１人はIT（情報技術）に何らかの形で関わることになると思います。そして、ITに関わる方々の10人に１人は重要なシステムに関わることになるでしょう。さらに、その中の10人に１人が、システムの設計に関わることになり、そのうえさらに、その内の10人に１人が歴史に残るような業績を残すようになると思っています。これは、私の主観で、勝手で大雑把な括りですが、その 1/10,000 に行き着くために代数学を学んで欲しいと思います。(*1)

1/10,000は小さい確率ですが、（一般的に）ヒトがその人生で出会えるヒトの数は 30,000人 と言われていますので、チコちゃんに「ボーっと生きてんじゃねーよ!」叱られながら (*2) 漫然と過ごしていても３人の「1/10,000」には出会えるということになります。それを期待しつつ書いています。

私は、一応理系と呼ばれる系統の人間ですが、数学者でも暗号学者でもありません。その私が代数学を語るなどおこがましいのですが、専門家ではない故に、皆さんに「少しは分かり易い」説明ができるのではと思いますので、今回は、このテーマで書かせて頂きます。

代数とは？

数を記号で表すことが代数。その言葉の通り、代数とは「数に代わる記号」で表現する世界です。コンピュータ、ひいてはシステムを動かすプログラムも同様です。なぜならば、変数を使って演算（計算）を行うのがプログラムというモノですから。

代数の基礎になる概念は何でしょうか？

それは「集合」です（集合を語るのであれば、シングルトン = 単元集合にも言及しては？ という親友？ 師匠？ からのご指摘もありますが、ここでそこを掘り出すと長くなるので、シングルトンに関してはまた別の機会にさせて頂きます）。

「公理」（公理系）を基点とする代数学では、その公理が適用される集合が明確に定義されます。数学で扱う集合とは、数の集合です。これらの集合に、二項演算（和、積）を加えたモノが「代数系」ということになります。

プログラムの話に繋げると、現在普及しているコンピュータと称されるモノのほぼすべては「整数」を基本とします（なにせ、0, 1 の組合せでしか数を表現できませんから）。コンピュータでも実数（小数）を扱えるじゃない？ と言うかも知れませんが、これは浮動小数点と言われる「なんちゃって実数」で、本来の実数が持つ稠密性は記述できない離散的な数値。数学的な表現をすれば「有限体」です。ここでの「体」は、球体とか立方体の「体」ではなく、「群・環・体」の「体」です。定義としては「有限個の元からなる体、すなわち四則演算が定義され閉じている有限集合」ということになります。

ということで、「整数論」「有限体」とその応用が重要です。

インターネットを含め、「通信」が不可欠な現代社会にとって欠くことができない「符合理論」「暗号理論」は「有限体」を土台としています。「符合理論」とは、情報をどうやって符号化し、効率良く、かつ信頼性のある通信を実現するかがテーマです。符号とは、データ圧縮、誤り訂正などを考慮した上で、情報を表現する方法ということになります。暗号化も、そこに含まれるとすると、符合理論 ⊃ 暗号理論 ということになります。

そのような背景から、これからの情報システムをリードしていく方々には、代数学の基礎は押さえておいて欲しい」という台詞になるのです。

代数って、理工系の大学の講義で出てくるけど、なんか良く分からないし、面白くない。全員がそう思っているとは言いませんが、少なくとも19歳だった私 (*3) は、そう思っていました。最初に「代数」に出会ったのは「線形代数」という講義でした。私の視野が狭かっただけですので、その講義内容を批判するつもりはありませんが、もう少し解きほぐし方があったのでは？ と今の私は思います。

もちろん、目指すところは「理論」を理解させる（する）ということになりますが、理論に重きをおくと、普通の学生にはハードルが高くなりそうな気がします。なので、最初のハードルは低くした方が良いのでは？ と思う次第です。多分に、あまり優秀とは言えない学生（= 当時の私）の経験に依りますが。

「線形代数」を理論的に表現すると「線形空間と線形写像を扱う代数」ということになります。確かに正しい表現ですが、大学１年生に対しての良い説明だとは思えません。もう少しザックリと表現するのであれば「行列を使って色んなことをする」と言い切っても良いのでは？ と思います。

「行列が分からん」と言われると別の表現も考えなければなりませんが、当時の高校の数学では「行列」を扱っていました。しかし、2012年度高校入学以降「行列」が高校の過程からなくなりました。そして令和４年から復活するそうです（迷走？）。これに関しては賛否がありますが、私は、どっちでも良いです。そもそも高校の教育と大学の教育の連続性がないので、個別の議論には意味がありません。その観点では、高等専門学校（高専）への期待が高まります。愚痴でした……。 「線形代数」の前に「行列」をキチンと教えるのが良いでしょうし、「線形代数」の前奏として「行列のおさらい」をやっても良いでしょう（教育には反復も必要ですし）。まずは、ラーメン屋や法律相談所にできる行列と、数学での行列は違うモノですよ、という説明から（笑）。

まずは、行列から、自然数から

行列は、複数の数が四角形に並んだもので、「写像」を考える上での便利なアイテムです。

「写像」も分かりづらいですね。元の値に対して何らか操作を行うことを、数学では写像と称します。例えば「x + 2 」は「x に 2 を加算する写像」ということになります。

f(x)=x+2

を定義すると、 f(x)は x に 2 を加算する写像関数」ということになります。

ここでの詳説は（本論から外れますので）避けますが、行列は連立方程式の記述に役立ちます（行列自体の出自がそこにあります）。また、画像処理や３次元データ処理（アフィン変換行列）、機械学習（ニューラルネットワークにおける演算）、量子力学（ハイゼンベルク描像）などで「行列」は欠くことができない要素です。行か列が「１」のものは「ベクトル」と呼ばれます。幅広い分野に関わります（どちらが「１」なのかは重要な意味を持ちますが、ここではその説明は省かせて頂きます）。さらに多次元配列とも言える「テンソル」があります。

これらを並べて書くと次のようになります。

（単一の数値である）スカラ ⊂ ベクトル ⊂ 行列 ⊂ テンソル

いきなり「線形代数とは！」と振りかぶるのではなく、「行列って、色んなことに使えて便利だね」という辺りを起点にすれば、もう少し「いいね！」が沢山もらえるような気がします。

また、「群・環・体」に関しても、いきなり定義を説くのではなく、せめて「数」というものを拡張していく流れや、具体的な例をゆっくり示していけば、これも「いいね！」が沢山もらえるかも知れません。

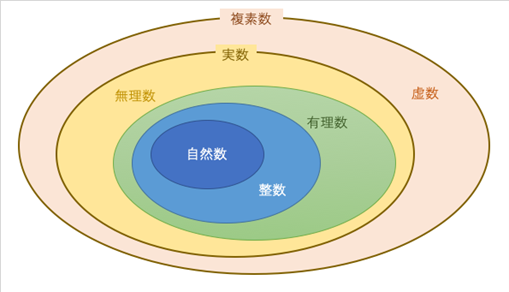
ヒトは、「数」の概念を（歴史の中で）拡張してきています。自然数 ⊂ 整数 ⊂ 有理数 ⊂ 実数 ⊂ 複素数 という形です。自然数 → 整数 → 有理数 → 実数 → 複素数 と（約4,000年という歳月をかけて）ヒトは「数」の概念を拡張してきました。「複素数」が頂点ではなく、「数」概念をさらに拡張したモノが「群・環・体」です。

ということで、プロローグとしては、改めて「自然数」からスタートというのもありなのでは？ と思います。

「数」の拡張（複素数まで）

最初は「自然数」ですね。

１、２、３、４、１０，１００といった、文字通り「何かを数える」ための「数」です。この「数」の集合が「自然数」です。

その拡張が「整数」です。

「りんごが５個ありました。５個食べました。残りはいくつでしょう？」の答えは「０個」です。ここで「０」が登場します。さらに「りんごが５個ありました。６個食べました。残りはいくつでしょう？」を考えます。「食べられへん！」という回答も正しいですが「１つ足りない」を表現するということで「−１」が登場します。ゼロとマイナスの「数」が追加された「数」の集合が「整数」です。

次の拡張が「有理数」です。
「りんごが６個ありました。３人で分けると、１人当たりはいくつでしょう？」
この場合の解は「２」で自然数の範囲です。
「りんごが６個ありました。４人で分けると、１人当たりはいくつでしょう？」

この場合の解は「2/3＝1.5」です。これは、整数の範囲も超えています。これが「有理数」です。小数点が付くかどうかではなく「分数」で表すことができる数を「有理数」と呼びます（小数でいうと、有限小数と循環小数ということになります）。

次の拡張が「実数」です。
ここまで来ると「りんご」では表現できません。話を端折って説明すると、分数では表現できない数が無理数です。

具体的には、√2やπが無理数です。有限小数でも、循環小数でもない小数ということにもなります。数として存在するが、分数での表現ができない数ということになります。 「有理数」と「無理数」を合わせた集合を「実数」と呼びます。

次の拡張が「複素数」です（りんごは出てきません）。　

√2 

つまり、２乗すると 2 になる数は確かに存在します。

たとえば、面積 = 2 の正方形の一辺の長さは
√2 になるので、実際に存在する数です。

しかし、√-2
つまり、２乗すると -2 を考えると「そんな数は存在しないよ」 というのは正しい感覚です。

「そんな数を定義して意味があるの？」という疑問も正しい感覚です。
しかし、必要な場面は、確かに存在します。

例をあげます。まずは、２次方程式です。

x²-8x+15=0の解は、x=3.5 です。

それでは、別の例です。

x²-8x+17=0

では、ｘを有理数に限定すると、解は存在しないということになります。

しかし i²＝-1

という数、つまり虚数を定義すると、解は
ｘ＝4±i　
となります。　　　
めでたく解けました。

なんか無理矢理、虚数を作って、解いたことにしているのでは？と言われると反論は難しいです。

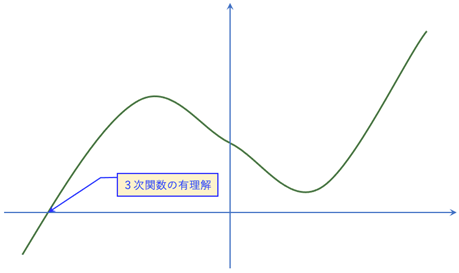
では、３次方程式です。どんな３次関数を定義しても、そのグラフを描くと必ず x軸 と交わります。これは、少なくとも３次方程式の解の１つは「必ず実数である」ということになります。

この実数解を α だとすると、三次方程式は、(x-α)(αx²+bx+c)=0 となります。 つまり、３次方程式の解は、α と ２次方程式 (αx²+bx+c) の解 ということになります。

ということは、（重解は２つの解だと考えることにすると）３次方程式の解は「３つの実数解」あるいは「１つの実数解 と ２つの虚数解」ということになります。

２次方程式の場合は、解は「２つの実数解」あるいは「２つの虚数解」なので、後者は解けないで済まされます。しかし、３次方程式の場合、１つ必ず実数解になるので、虚数解があるからといって解けないでは済まないぞ。ということで、虚数を認めようという話になったとか、ならなかったとか。

16世紀、数学者カルダノさんの業績です。哲学者であり数学者でもあるデカルトさんは、この虚数に関して否定的だったそうで「空想上の数」と呼びました。皮肉なことに、これが imaginary number の語源となり、虚数は「i」と表現されるようになりました。

そして、18世紀、オイラーさんの登場です。円周率の「π」、三角関数「sin,cos」、対数「log」、自然対数の元でネイピア数 の「e」、そして虚数「i」。既出のこれらの概念に加えて、無限大「∞」が、オイラーさんの著書「無限解析序説」の中で１つに統合されます。

e^ix=cos⁡(x)+i∙sin⁡(x)　…　オイラーの公式

この公式に至るまでの、すべての系譜に意味がありますし、オイラーさんご自身の辿った道も美しく興味深いのですが、それを語りだすとキリがありませんので（泣く泣く）ここでは割愛します。

波動を扱う振動学にも虚数は必須ですし、交流回路にも虚数は不可欠です。何が言いたいかというと、虚数もこの世界を表す要素の１つだと言うことです。実数に虚数も加えた「数」の概念が「複素数」です。

やっと、ここまで来ました。「数」の拡張は、「群・環・体」の入口まで辿り着いたので「プロローグ」としては、こんなところです。１話分の文字数の限界を既に超えていますし。

まとめ

今回は「数学を学ぼう！」感、満載でお届けしましたが、如何でしたでしょうか？　「数学はいいから、もっとCyber Securityをネタにしろよ！」と言われそうな気もしていますが、せっかくここまで来たので、「群・環・体」まで進めておきたいので、もう１話だけお付き合いください（と言いつつ、ＣＳ（サイバーセキュリティ）に戻せ圧が強い場合は、日和るかも知れませんが（苦笑）。

---

(*1) ソフトウェア・エンジニア

脱線になるので、こちらに「独り言」を書きます。綺麗なプログラムを書くためには、代数的な発想の上に、構造化の概念が必要です。もちろん代数にも、より原理的な「構造」が存在しますが、 プログラミングで要求される構造は、それとは少し異なります。（ハードウェア、OS、プログラミング言語などによって作られる）現実と共存可能な構造が必要ですから。

それらを踏まえた上で、システムを設計するためには、要求仕様の把握、高次元の構造化のほか、（予算、納期、使える工数など）大人の事情も考慮する必要があります。美しい代数の世界から外れて行ってしまいますが、現実は美しさとは無縁な猥雑な世界であるという達観も要求される訳です。残念ながら……。

(*2) チコちゃんに叱られる

ある意味、商業スポンサがいないので尖った番組を作れるNHKらしい番組で、雑学を学ぶのに良い時間なので、私は好きで、ほぼ欠かさず観ています。
https://www.nhk.jp/p/chicochan/

(*3) 19歳 大学に進学し19歳になった私は、友人も親戚も一人もいない寒冷な新天地で独り暮らしを始めたばかりでした。共同玄関・共同トイレの生活にも慣れなければならないし、自炊もしなければならないし、そこそこ授業のコマ数も多いし、クラスの仲間ともつるまなきゃだし、「軽音」に入りバンド活動も始めたし……で、線形代数は頭に入る余地がありませんでした。「大学生と言っても、まだ未成年だし！」といいつつ、私が大学生だった時代は（法律的にはNGですが）「大学生は飲酒OK」というノリでした。入学直後は「新歓コンパ」なるものが複数あり、そこで「大酔っ払い」を実体験していくことになります。あっ、これも代数学が頭に残らなかった原因かも知れません（←こういうのを詭弁といいます）。時代が変われば、こうした風景も変わりますね。2022年の（通常の）大学生は18歳で既に成年になっている訳ですし、今の時代、かつてのように飲酒に寛容ではなくなりましたから、成年とはいえ20歳になっていない大学の新入生は「大酔っ払い」を体験することはないので、代数学が頭に入りやすいかも知れません（←これは詭弁ではなく、謬論？！）。

---

白狐村塾話の過去の記事はこちら（合わせてお読みください）
ＣＳ白狐村塾（第１話）サイバーセキュリティに必須の技術、詳細に解説！　その1
ＣＳ白狐村塾（第１話）サイバーセキュリティに必須の技術、詳細に解説！　その2
ＣＳ白狐村塾（第２話）楕円曲線暗号について
ＣＳ白狐村塾（第３話）基礎から徹底解説！　ストリーム暗号とは何か？　RC4から、Salsa20、ChaCha20まで

サイバーセキュリティ白狐村塾は、新たなお話が公開されたときにメールマガジンにてご案内致します。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。