暗号を理解するための数学の世界 ＣＳ四方山話（第34話）

「小学校からの数学」シリーズ・第13弾です。　前回予告の通り、今回も小学４年生で「計算の順序」と「折れ線グラフ」がテーマです。執筆としては、前回から３ヶ月以上空くことになっております。

仕事にかまけて「ＣＳ四方山話」をサボっていた訳ではありません。また別途、正式にアナウンスさせて頂きますが、「ＣＳ四方山話」を電子書籍化するという動きがありま、その原稿を作成するために時間を費やしておりました。ということで、ご容赦くださいませ。

計算の順序における2つのルール

さて、小学４年生で「計算の順序」として習うことは、以下の２つです。

　・　掛け算と割り算を、足し算と引き算よりも先に計算しましょう
　・　基本的には、左から順番に計算しましょう

英語圏では「PEMDAS」と呼ばれます。

　➢P = Parentheses first
　➢E = Exponents (ie Powers and Square Roots, etc.)
　➢MD = Multiplication and Division (left-to-right)
　➢AS = Addition and Subtraction (left-to-right)

上記の頭文字を並べたもので、この順番に計算しましょうということです。

まず、P = 括弧が最優先で、次に指数（べき乗、平方根など）、次に掛け算・割り算で左から、最後に足し算・引き算を左からということになっています。

同列でない加減乗除における計算の方法

基本的な計算（演算）の方法は、加算（加法）「＋」、減算（減法）「−」、乗算（乗法）「×」、除算（除法）「÷」の４つです。四則演算と呼ばれます。

しかし、この４つの演算は同列ではありません。

例えば、「自然数」は加法と乗法に関しては閉じています。自然数同士を足しても自然数になりますし、自然数同士を掛けても自然数になります。これが「閉じている」ということです。

自然数同士の減算は、自然数になるとは限りません。例えば、「４」から「６」を減算すると、結果は「−２」となります。「−２」は、自然数ではなく整数です。「自然数に関しては加法、乗法に関しては閉じている」ということになります。

計算の対象を「整数」とすると、加法、減法、乗法に関して「閉じて」います。しかし、「除法」に関しては閉じていません。「４」を「６」で割ると、結果は「4/6 (= 2/3)」で、これは整数ではありません。

「有理数」に範囲を広げると、加法、減法、乗法、除法のいずれに関しても「閉じている」ということになります。

また、「減法」は「加法」の逆演算と考えることができます、「除法」は「乗法」の逆演算と考えることができます。

「乗法」は、元を正せば、「加法」の繰り返し演算です。「４ × ６」は「４ + ４ + ４ + ４ + ４ + ４」という意味です。そして「除法」は「乗法」の逆演算です。

さらには「べき乗」は「掛け算」の組み合わせです。「4 ^ 3」は「４ × ４ × ４」という意味です。「平方根」は、２乗の逆演算です。

再び、計算の順序についての考察

掛け算・割り算が、足し算・引き算に優先する理由は「単位を揃えないと、足し算・引き算ができないから」と言われたりもします。

「現在の手持ちが 800円 です。１個240円のリンゴを2つ買うと、いくら残るでしょう」

　800円 – 240円 × ２個 = 800円 – 480円 = 320円

日常生活で出てくる場面として想像しやすいのですが、掛け算・割り算を行ったから単位が揃うとは限りません。

「現在の手持ちが 800円 です。2時間で12km歩きました。いくら残るでしょう」

　800円 – 12km ÷ 2時間 = 800円 – 6km/毎時 = ？？？

「PEMDAS」を眺めてみるに、計算の順序が明示されない場合は、より複雑な組み合わせの演算を優先で計算して、より基本的な演算は後回し、同じ優先順位のものが並んでいたら左から計算する。そのように解釈できます。

「慣習」としての計算順序の結論

単位がどうとかはアテになりませんし、なぜ組み合わせ演算を優先するのかにも、左から計算するのかにも根拠はありません。結局は単なる「慣習」なのです。

だったら、論理的な根拠を持たない「計算の順序」なんぞを「柔軟で将来生のある若人に擦り込む」ことは正しいと思えませんので、誰もが計算の順序を間違わないように「必ず括弧を付けましょう」と教えるべきなのでは？　と筆者なんぞは思う次第です。

時系列データで使われる折れ線グラフ

折れ線グラフの２軸は、自由に選択できる訳ですが、横軸は「時間」に設定される場合が多いようです。これは、折れ線グラフの表現の特性上で「時系列の連続性のある変化」を視覚的に表現する上で効果的だからだと思います。

小学４年生の学習の例では、横軸は時刻（気温の変化）、月（体重の変化、平均気温の変化）が登場しています。折れ線グラフでは、線が右上がりなら値が増加しており、右下がりであれば減少していることを視覚的に捉えやすいという特徴があります。数学的な言葉で表現すると、微分値が正か負かということになります（小学４年生向けの表現ではありませんが）。

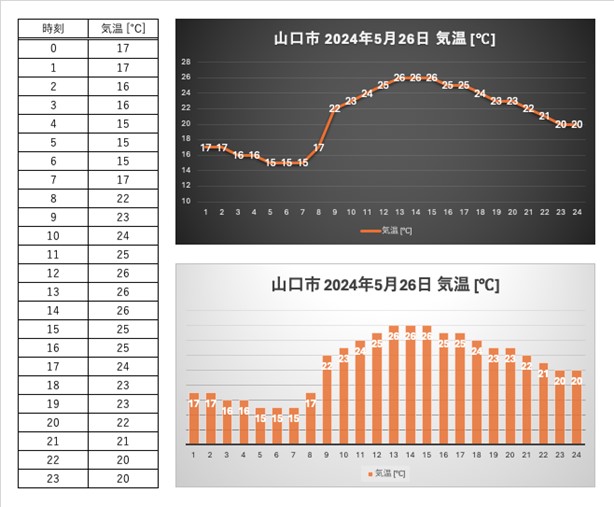
やはり、時系列データのグラフが「折れ線」が良いですね

まとめ

今回は、小学４年生の課程の「計算の順序」と「折れ線グラフ」を勉強しました。次回（第35話）からは、小学５年生に進級します。「小学校からの数学」シリーズも終盤ということになります。引き続き、ご購読頂ければ幸いです。

---

四方山話

今年（2024年）に起きた、サイバーセキュリティ上の大きな問題が２つあります。大きな問題かどうかは意見が分かれるところだと思いますが、システムも重要な機能に関わる問題であると共に、OSS (Open Source Software) の信頼性の根幹に関わるため、「大きな問題」と言って良いと考えています。

【XZ Utils 問題】

１つ目は「XZ Utils にバックドアが仕込まれた件 (CVE-2024-3094)」です。XZ Utils は、主な Linux のディストリビューションで採用されている圧縮ツールです。この圧縮ツールにバックドアが仕込まれ、サーバーなどへのログインに広く用いられている SSH (OpenSSH) も影響を受け、特定の条件下ではありますが、遠隔から任意のコードを実行可能となります。

幸いなことに、あるエンジニアが sshd（ssh ログインを処理する機能）が通常よりもCPUの使用率が高いことから偶然に発見したことで、多くの Linux のディストリビューションに適用されリリースされる前に対策されました。

多用されているツールに重大な脆弱性があったということも問題ですが、人為的にバックドアが仕込まれたこと、そのバックドアを仕込んだ人物は約２年という時間を費やして、XZ Utils に関わり、さまざまなプルリクエスト（改善提案）やバグ修正に関わることでプロジェクトでの信頼を積み重ね、リポジトリの権限、コミット権限を獲得し、遂にはリリースマネージャーの権限も獲得しました。ある意味信頼関係で成り立っている OSS の開発の在り方に課題を投げかけることになりました。

OSS のメリットは、ソースコードが公開されており、その透明性が高いことにあります。しかし、今回の場合は、リリースされるバイナリと公開されているソースコードが厳に紐付いていることを保証するところに綻びが生じたことになります。今回のような事態を回避するためには、第３者がソースコードを監査し、監査したソースコードを第３者がクリーンな環境でビルドして、署名した上でリリースするといったプロセスを確立する必要があると考えます。

【PuTTY 問題】

こちらも SSH に関連する問題で、PuTTY は Windows 用の SSH クライアントです。ここでは詳細には触れませんが、授受されるメッセージから、SSHログインに必要な秘密鍵を窃取できる可能性があります。修正されたバージョンにアップデートすることも必要ですし、秘密鍵の窃取が疑われる場合には、秘密鍵を作り直すことも必要となります。

SSH に馴染みのない場合には、なんのこっちゃかも知れませんが、SSH は筆者のような開発やシステム管理を行う者にとっては必須のツールです。これを使って、さまざまなサーバーやネットワーク機器やPCなどに入って作業をするため、ここがダメダメな場合は簡単にシステムやサービスを乗っ取れることになるので「大問題」になります。

---

ＣＳ四方山話の過去の記事はこちら（合わせてお読みください）

サイバーセキュリティ四方山話の最新話は、メールマガジンにてもご案内致しています。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。