CS四方山話(第22話)暗号を理解するための数学の世界 その1
小学生からの数学シリーズ
昨年11月から約4ヶ月、間が空いてしまいました。CS四方山話のファンの皆さま(そんな方、いるのかな?)大変お持たせしましたが、ボチボチ再開です。
前回(第21話)で「次回は暗号の話」と宣言しましたし、その方向で原稿を書いたのですが、なかなか分かり易くならない……という辺りで、書いてみてボツにしてを繰り返していました。実際には、もう1つ理由があって、1月末まで仕事が立て込んでいまして……。まあ、いつでも忙しくて原稿を書くのは、休日か夜間なのですが、そこまで仕事がはみ出していたということになります。
いずれにしても言い訳ですので、この話はここまでにして本題です。
暗号を理解するには数学の知識から
いきなり「暗号」の話を分かって頂こうという点に無理がありました。
「CS白狐村塾」で筆者自身が書いていたのですが「暗号化方式は、数学の世界です」。「暗号」を説明する前に、数学の世界に触れてもらおうという方向に舵を切ろうという方針にしました。
これには、もう1つの狙いがあります。
IT (Information Technology) も、ICT (Information and Communication Technology) も、インターネット (Internet) も、その土台になっている 計算機 = Computer も、計算機を動かす プログラム (Program) も、その動作を支えている理屈は「数学」です。
これからその世界を担ってくれる若い方々には、是非、数学を好きになって欲しい。無理なく、数学を学んで欲しい。そのためには、何かしら参考になるモノ(教科書とは言いませんが、読本のようなモノかな)があると良いのでは?と思っています。
いきなりそんな大それた事は無理でも、試しに何か書いてみようというのが「もう1つの狙い」です。あまり数学に親しくない大人の方々に分かり易ければ、小学校、あるいは、中学校の皆さんにも分かり易いかなということで、この「CS四方山話」の場をお借りして試してみようと考えた次第です。
小学1年生で学ぶ算数(数学)
多くのヒトは小学1年生ではじめて「算数」という形で「数学」に触れるのだと思います。その小学1年生の算数の授業で何を教わるのかをみてみましょう。
小学1年生は、平面、立体の図形の種類や大きさの比較、時計の読み方などに関しても学びますが、メインディッシュは整数の足し算・引き算です。
まずは、ここから探っていきましょう。
実際に、小学1年生で扱う数は、0(zero)と自然数です。列挙すると、0, 1, 2, 3, 4 .. となります。言い換えれば、0(zero)と正の整数ということになります。
小学1年生で教わる数なので、「自然数」=「正の整数」= { 1, 2, 3, 4, .. } に 0 (zero) を足した { 0, 1, 2, 3, 4 .. } という括りにも名前があると良いのに〜と思ったりします。実際には、大学の数学では、自然数を { 0, 1, 2, 3, 4 .. } と定義することが多いです。この辺りも、数学につまずく要因の1つです(小学校と大学とで自然数の定義が異なるのはよろしくありません)。これから、日本では「新解釈」として、自然数を { 0, 1, 2, 3, 4 .. } として教えましょう!(と、勝手に決める)
ちなみに、英語では 整数は integer です。直訳すると自然数は natural number となりますが、これは忘れちゃいましょう。
では、新解釈「自然数」は英語ではなんと表現するのでしょう。それは、unsigned integer(符号なし整数)、縮約(しゅくやく)すると 「unsigned int」 です(プログラミングをする方々にはお馴染みの表記ですね)。ほら、これでプログラミングにもスムーズに進めそうな気がしてきました。
足し算・引き算は、数学的には「加法」ということになります。加えている(加算)だけではくて、減らしている(減算)もしていると思うかも知れませんが、数学では「逆元」という考え方があるので、加算も減算も「加法」として扱います。
6 – 3 = 6 + (-3)= 3
-3 は 3 の「逆元」です。これで、引き算も「加法」として扱えることも学びました。
概念的には「3 を引く」は「3 を足すことの逆をやるのと同じ」ということです。「3 を足したら 6 になった。では、3 を足す前はいくつだったのか?」というように、逆方向に操作を行うということになります。この「操作」を「演算」と書き換えれば、数学っぽくなります。
小学1年生で「0」を扱います。「0」は、足しても、引いても値は変わりません。
6 + 0 = 0 + 6 = 6
6 – 0 = 6 + (-0) = (-0) + 6 = 6
6 – 6 = 6 + (-6) = 0
この「0」は、加法における「単位元」です。
数学的な表現を採ると、集合 A の元の間に定義された結合法(演算)を ☆ とするとき,A に属する一つの元 e と A に属する一つの元 x に対して常に下記が成立する時「e」を単位元といいます。
x・e = e・x = e
「0」を発見したのはインドの数学者だったとか、いやいや、仏教ではそもそも zero =「空」という概念があったとか、「因果」は量子力学に通じるとか、この辺りの話も深掘りするとキリがないので、置いておきましょう。
まとめ
文字数も良い感じになりましたし、リフレッシュ後1回目はこんなところで。
次回も「楽しく学べる数学」を目指します。
上記で登場しなかった数学的に大切な特性が2つあります。「閉じていること」と「結合則」です。これを次回(小学2年生、というか新解釈・小学一年生)でみてみましょう。そこまで進めば、あなたも、理系の大学で学ぶ「群」を理解したことになります。ついでに、小学校1年生で躓きがちな「繰り上がり」「繰り下がり」に関しても考えてみましょう。
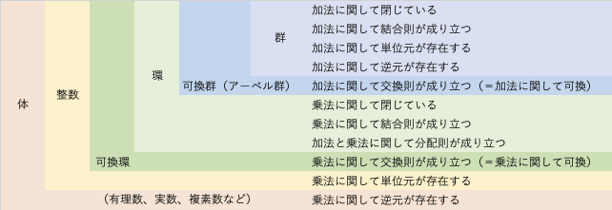
「群」の先は「CS白狐村塾」第5話に書いた下図の通り「環」「体」と続きますが、恐れることはありません。「環」も「体」も(新解釈の)小学校の課程で学べますから。
四方山話
昨年のJAPANSecuritySummit 2022のLiveセッション で、島根県益田市さんがGIGAスクールを基点とした、ICTリテラシー啓発、サイバーセキュリティ教育に取り組まれていること知りました (*1)。そして、今年(2023年)の2月に、益田市の皆さんのご好意で、その現場を訪問させて頂きました。
小学1年からタブレットを使った授業を行い、小学5年からはMS Officeを使いこなす。授業後に、海外とWeb会議で接続して海外の生活に触れる。中学校の授業では、他校の生徒もオンラインで参加して話をしながら、新しいスポーツのルールを考案する。そうした創造的な活動を、市や地域が一体となって支える。とても素敵な現場でした。
この話を書き出すと「CS四方山話」数話分になってしまうので、この辺りで止めておきますが、こうした活動を持続化させるためには、そのコミュニティが維持されること、すなわち、経済的な活性を維持・向上することが条件となります。そのためには「地方の真に豊かな環境で暮らし、世界トップレベルの報酬を得る」ことが必要で、それにはネットワークを活用した仕事を地方に根付かせることが必要だと考えています。
そのためには、小学校から数学を、きちんと身に付くように分かり易く学ぶこと、学べる環境を醸成することが近道だと思っています。
(*1)
GIGAスクール時代のICTリテラシー啓発、サイバーセキュリティ教育「さあ、ここからが本番だ!」JAPANSecuritySummit 2022 Liveセッション
https://japansecuritysummit.org/2022/10/5236/
(注:このセッションは終了しております)
GIGAスクール時代のICTリテラシー啓発 教育現場の声 益田市編
JAPANSecuritySummit Update の 連載で第1話は下記です。
CS四方山話の過去の記事はこちら(合わせてお読みください)

中村 健 (Ken Nakamura)
株式会社SYNCHRO 取締役 CTO
機械屋だったはずだが、いつの間にかソフト屋になっていた。
以前は計測制御、知識工学が専門分野で、日本版スペースシャトルの飛行実験に関わったり、アクアラインを掘ったりしていた。
VoIPに関わったことで通信も専門分野に加わり、最近はネットワークセキュリティに注力している。
https://www.udc-synchro.co.jp/
サイバーセキュリティ四方山話の最新話は、メールマガジンにてもご案内致しています。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。


