暗号を理解するための数学の世界 CS四方山話(第36話)
「小学校からの数学」シリーズ・第15弾です。前回に引き続き、小学5年生です。最近、執筆の周期が長くなっております m(_ _)m 2024年中に小学校は卒業できるかな? と思っておりましたが、小学6年生は2025年に持ち越しとなりました。
「CS四方山話」の電子書籍 第1段「サイバーセキュリティ四方山話 VOL.1」は、無事、10月1日に ConTenDo さんから発売になりました。よろしければ、お手にとってご覧ください。
https://contendo.jp/store/contendo/Product/Detail/Code/J0010582BK0159582001
第2段も鋭意執筆中です!
図形の角度を求める
小学5年生では、図形に関する項目も複数登場します。まずは「図形の角」です。
角度に関しては、小学4年生で登場しました。このCS四方山話では第32話(https://japansecuritysummit.org/2024/01/9047/)でお話しましたね。小学5年生では、角度と図形の関係を学びます。ただし図形は、果たしてサイバーセキュリティに関係するのか? と自問してみると、う〜ん「あまり関係ない」となります。
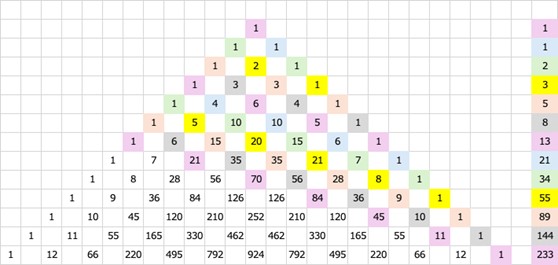
「三角形」と「整数論」とを無理矢理つなげるとすれば「パスカルの三角形」が登場します。

この「パスカルの三角形」は、nCm で表現される「組み合わせ(combination)」と密接な関係があります。また「二項係数」は「パスカルの三角形」の数値と同じで、「二項定理」とも関連します。(※1)
このテーマも非常に面白いのですが、小学5年生の「図形の角」とは完全に乖離します。ひとまず「パスカルの三角形」に関しては置いておきましょう。話を小学5年生の世界に戻します。
最初に登場する図形は三角形です。なぜならば、最も単純な(頂点も辺も最小の)図形は、三角形だからです。
三角形の内角の和は 180度 です。「度」は何なのかは「補足」に記載します。(※2) また、三角形の内角の和が180度であることの証明は、中学2年生で登場します(CS四方山話が続いていれば、中学2年生の回で取り上げさせていただきます)。
ということで、前置きが長くなりましたが、小学5年生で扱う図形の角度の問題は、基本的には「与えられた式に合致する変数の値を求める」問題ということになります(変数を使った式の話は中学生の話ですが……)。
たとえば、2つの角度が分かっていたとします。ここでは、90度と60度としましょう。
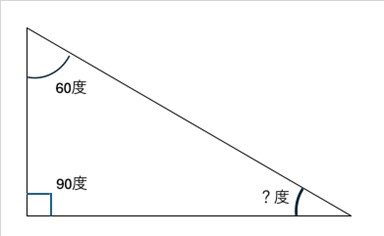
合計すれば180度になる訳ですから、次の式で答えが求まります。
180-90-60=30
この問題を一般化すると(小学5年生の範囲からはみ出していますが)、次の式となります。
a+b+c=180 ただし、a, b, c は、三角形のそれぞれの角の角度とする
この一般化を当てはめると、次の式となります。
a+90+60=180
a=180-90-60
a=30
もう少し捻った問題にしましょう。二等辺三角形だとします。等辺のなす角度が 90度 だとします。残りの2つの角の角度は何度でしょう。
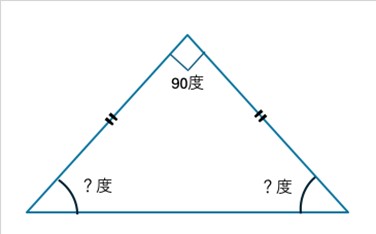
二等辺三角形なので残りの2つの角の角度は同じで、3つの角度を合計すれば180度になる訳ですから、次の式で答えが求まります。
( 180-90 )÷2=45
一般化を当てはめると(小学5年生の範囲からはみ出していますが)、次の式となります。
a × 2+90=180
a × 2=180-90
a × 2=90
a=90÷2
a=45
合同な図形とは?
合同とは、「平行移動や回転、反転などによって、一方の図形を他方の図形にぴったり重ね合わせることができる関係」を指します。形状が同じでも、大きさが異なる場合は合同とはなりません(形状が同じで、大きさが異なる図形は「相似形」です。これは中学生で登場する項目です)。
合同な三角形の条件は以下の通りです。
・ 3組の辺がそれぞれ等しい
・ 2組の辺とその間の角がそれぞれ等しい
・ 1組の辺とその両端の角がそれぞれ等しい
次の2つの三角形は、平行移動と回転だけでは重ね合わせることができません。
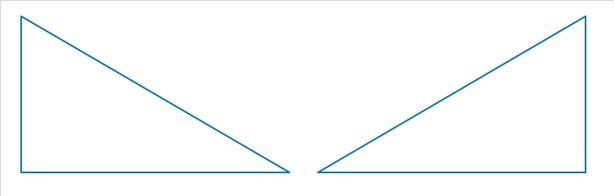
しかし、反転させると重ね合わせることができるので「合同」ということになります。個人的には、「反転」はズルで、この2つの図形は「合同」ではなく「2次元上の鏡像異性体」と呼ぶべきでは? と思っています。(※3)
今回は、小学5年生の課程の「図形の角」と「合同な図形」を勉強しました。下記の「補足」含めかなり脱線が多いと自覚していますがご容赦ください。
次回(第37話)は、引き続き小学5年生図形に関してとなります。小学5年生の課程には、平面図形や立体図形などの話題もあります。引き続き、お読み頂ければ幸いです。
補足
(※1)パスカルの三角形

パスカルの三角形は、いろいろな数学の話に関連します。二項係数(二項展開の係数)もパスカルの三角形の各列の値になります。
$$ (x + a)^n = \sum_{k=0}^n \binom{n}{k} x^k a^{n-k} $$
$$ (x + a)^2 = x^2 + 2ax + a^2 $$
$$ (x + a)^3 = x^3 + 3ax^2 + 3xa^2 + a^3 $$
また、パスカルの三角形の奇数部分を塗りつぶすと「シェルピンスキーのギャスケット(フラクタル図形)になります。


また、左側から右下斜めに数字を拾って合計すると「フィボナッチ数」になります。1から始めて前の数字を加算していく数列で、隣り合う2つの数字の合計が次の数字になります。
(※2) 度(角度の度)
角度が一周で360度であるのは、古代メソポタミアのバビロニア人がそう定めたからと言われています。バビロニア人は、太陽が同じ位置に戻るまでに365日かかること、月が同じ位置に戻るまでに355日かかることを把握していました。その中間が「360」となることと、「360」は24個もの約数を持つことから「360度」と決めたようです。
(※3) 鏡像異性体
私が化学を習った頃は「光学異性体」と呼称されていました。現在でも高校の授業では光学異性体と呼ばれています。乳酸やアラニンの異性体では旋光性(直線偏光が物質を通過するときに偏光面を回転させる性質)が異なることから、そう呼ばれています。しかし、学会や大学では光学異性体という単語は使わず、鏡像異性体と呼びます。教科書の慣性力が大き過ぎる悪例の1つだと思います。
四方山話
昨年(2024年)の年末(12月26日)には、日本航空(JAL)さんと、三菱UFJ銀行(MUFG)さんへのサイバー攻撃が発生しました。どちらも DDoS(Distributed Denial of Service、分散型サービス拒否)でした。DDoS攻撃とは、ターゲットに対して多数のコンピュータやIoT機器から大量のパケットを送り込み、ターゲットの正常なサービスの実行を阻害する(邪魔する)攻撃になります。
JALさんでは、手荷物預かりシステムや予約システムなどが一時的に停止しました。MUFGさんでは、オンラインバンキングなどのサービスにつながり難くなるなどの障害が発生しました。基本的には、サービスを邪魔する攻撃で、いずれも 5~6時間で復旧し、データの流出などは発生しませんでした。
ただ、気を付けなければならないのは、DDoS攻撃は繰り返し行われることもあることと、ランサムウェア攻撃やデータ窃取などの攻撃のための陽動として DDoS攻撃を行うこともあることです。今後、こうした重要インフラへの攻撃が続くことに警戒する必要があると考えています。
雑談
筆者は、年末年始は、東京で過ごしました。本年もよろしくお願い致します。
表参道が明治神宮に辿り着くところにある神宮橋は、知る人ぞ知る「初日の出スポット」です。
元旦の朝もそれなりに人が集まっていました。表参道のお陰で、都内としては非常に見通しが良く、早めに初日の出を拝めます。もちろん都内で最早で初日の出を拝むには、スカイツリーに昇るのが一番ではあります。ちなみに、冬至の日には、表参道の軸線上に日が昇ります(そうなるように表参道の方角を決めた?)。東京の日の出は 6:51 ですが、見通しが良いとはいえ遮蔽物があるので、初日を拝めたのは 6:58 頃でした(山口での初日の出は 7:20 だったそうです)。

CS四方山話の過去の記事はこちら(合わせてお読みください)

中村 健 (Ken Nakamura)
株式会社SYNCHRO 取締役 CTO
機械屋だったはずだが、いつの間にかソフト屋になっていた。
以前は計測制御、知識工学が専門分野で、日本版スペースシャトルの飛行実験に関わったり、アクアラインを掘ったりしていた。
VoIPに関わったことで通信も専門分野に加わり、最近はネットワークセキュリティに注力している。
https://www.udc-synchro.co.jp/
サイバーセキュリティ四方山話の最新話は、メールマガジンにてもご案内致しています。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。