暗号を理解するための数学の世界その10 ＣＳ四方山話（第31話）

小学校からの数学シリーズ・第10弾

「小学校からの数学」シリーズ・第10弾です。「小学生シリーズ」も10話になりました。今回で、小学３年生の課程は修了となります。今回のお題は「小数」と「分数」です。どちらも日常生活にも登場してくる一般的な概念ですが、いつものように少し掘り下げると「数学」が顔を覗かせてきます。

16 – 17 世紀ごろに発明された小数の概念

数値の表記として、数値を表現する文字が足りなくなると、桁数を増やして表現するという方法を採ることを、いままでの課程で学んできました。

10進数を表現する文字 = { 0, 1, 2, 3, … 8, 9 }

“1”, “2”, “3” … “8”, “9”、ここまでくると次の文字がないので”10″ と表現します。左側2桁目に書いた数字は（10進数なので）
10 を表していることにします。

左側に桁数を増やしていくことで、大きな数を表現できるようになりました。

では、1 よりも小さい数値はどのように表現すれば良いでしょうか？　小さい数値も、いろいろあります。1 を 半分にする、1 を 10等分 するなどで 、1 よりも小さい数値になります。

「.」を打つことで、1よりも小さい数を表現するための「桁」を容易しました。下記のようなことになります。

1 × 10¹+ 2×10⁰ + 3×10^-1+ 4×10^-2

＝1×10+2+3×\(\frac{1}{10}\)+4×\(\frac{1}{100}\)
＝12.34

点を一つ記述することで「桁」の概念を拡張できるので、非常にシンプルで分かり易い表現ですね。この「小数」の表記方法が「発明」されたのは、それほど昔のことではありません。16 – 17 世紀のことです。

分数を少数で表現すると……

分数は、考え方としてはシンプルなモノです。例えばリンゴが２つありました、これを５人で分けるとしたら、１人当たりはいくつになるでしょうか？　分数の表記が許されれば答えは簡単です。2/5で、問いの内容そのままですね。

2/5は、小数でも表現可能です。

2/5＝\(\frac{2}{5}\)＝\(\frac{4}{10}\)＝4×10^-1=0.4

問題を変えてみましょう。リンゴが２つありました。これを３人で分けるとしたら、１人当たりはいくつになるでしょうか？（さっきよりも分け前が増えたことは確かです）　分数を使えば、やはり答えは簡単、2/3 です。

これを小数で表現するとどうなるでしょうか？　10進数の「10」と、除数の「3」が公約数を持たないので、先程のように簡単には行きません。

結論から言うと、0. 6666666 … と終わりなく「6」が連続する形になります。小学３年生の課程には、この「ややこしい」パターンは登場しませんが、このパターンは「循環小数」と言われるものです。表現形も用意されており、循環する部分の頭に「・」を付けます。

ところで、分数には複数の種類があります。

真分数、仮分数、帯分数
　
この分類、筆者は「な〜んとなく」程度の記憶しかありませんでした。きっと覚えなくても良いことだと思いますが、小学３年生の教科書には登場するようなので、サラッと説明しておきます。

真分数の例 : \(\frac{2}{5}\)分母が分子よりも大きい分数です。

仮分数の例 : \(\frac{7}{5}\)分子が分母よりも大きい分数です。

帯分数の例 : 1 \(\frac{2}{5}\)整数＋真分数となる形態の分数です。

分数の本質は「比」の記述である！

分数は、その上記からも分かる通り「比」の記述です。これを２次元平面で記述すると、直線になります。

　 例えば、2/3 は、原点を通る、傾き 2/3 の直線として表現可能です。この直線は、(3, 2) を通りますし、(6. 4)、(9, 6) などを通ります。これは、3 : 2 = 6 : 4 = 9 : 6 というように比が同じということです。つまり、分数とは「比」の記述ということになります。

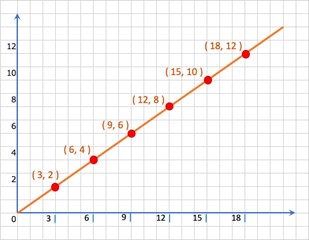
4/6 も 6/9 も、2/3 と同じですので、2/3 にまとめることができます。　これを「約分」と言います。約分をもう少しキチンと定義すると、それは「素数同士」の比にすることになります。

さて、もう一度、２次元平面で原点を通る直線を考えてみましょう。

(3, 2)、(6. 4)、(9, 6) のように、x, y が整数である格子点を通る「直線」は分数で表現できます。

ここで、少し傾きを変えてみましょう。今回は、少し直線を「寝かせる」ほうに変更します。すると、その直線は (3, 2)、(6. 4)、(9, 6) を通らなくなります。しかし、ずっと辿っていくと、格子点を通る場所が見つかりました。 それは、( 71, 107 ) でした。小数で表現すると ≒ 0.663551402

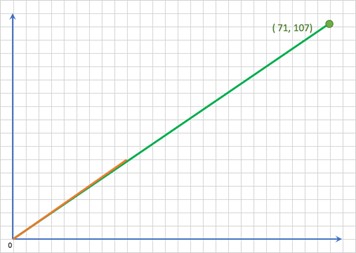
さらに、直線を「寝かせて」みましょう。なかなか格子点を通りませんね。しかし、ずっと先のほうで、やっと格子点を通りました。それは、( 66301, 99989 ) ≒ 0.663082939 です。

このように格子点を掻い潜って、なかなか格子点を通らない直線を探していくことが可能です。

これは、「より大きな素数を探すこと」と等価（同じこと）なのです。原始的な方法でも、無限にある（*2）大きな素数を探して行くことが可能です。

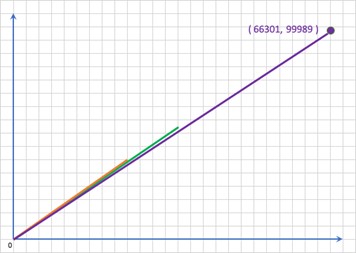
どこかで格子点を通る直線で素数を探せることが分かりましたが、どこまで行っても格子点を通らない直線を引くことも可能です。どこまで行っても格子点を通らないということは、分数では表現できないということになります。　

そのような直線の傾き = 「数」は「無理数」と呼ばれます。逆に、分数で表現できる数は「有理数」と呼ばれます（この話は、小学３年生の範囲は逸脱していますが..）。　

無理数の例としては、π = 3.14159265359..、\(\sqrt{2}\)= 1.414213562373095.. などがあります。πや\(\sqrt{2}\)が無理数であることの証明もされています（*3）。

まとめ

これで小数、分数についても学ぶことができました。小学３年生の課程は修了です。小学生の算数の半分を消化できたことになります。次回（第32話）からは、小学生の後半戦に突入します。小学４年生では、四角形、直方体といった図形も登場します。なぜ、小学４年生でこれらの概念が登場するのか？　も含めて、この辺りから数学を攻めてみたいと思います。

---

参照

(*1) 「ＣＳ四方山話（第27話）」の URL は下記の通りです。

ＣＳ四方山話（第27話）　暗号を理解するための数学の世界その6

Simon Stevin (1548-1620) が最初に発明したそうです。例えば、12.3456 は下記のように記載されました。

　　　12⓪3①4②5③6

これは、分かり易いとは言えませんし、文字数が増えます。

同じように感じた（であろう）John Napier (1550-1614) は別の表記法を「発明」します。それが、いま我々も用いている「小数点」を使った表現です。

Napier = ネイピア。聞き覚えがある名前ですね。そうです、John Napier は「対数」の研究を行っており、自然対数 ｅ の近似値を論文に記載していました。この事実から、ｅ を「ネイピア数」と呼びます。ただ、ｅ は（18世紀の数学者オイラーにちなんで）「オイラー数」とも呼ばれます。ｅ は Euler の頭文字だそうです。ちなみに、厳密に ｅ を定義したのは Jakob Bernoulli (1654- 1705) で、複利の計算で求めようとした下記の値が ｅ でした。なんか話がややこしいですが、そういうことだそうです。

$$e = \lim_{n \to \infty} \biggl( 1+\frac{1}{n} \biggl)^{n}$$

(*2) 素数が無限にあることの証明方法は複数あります（興味のある方はネットを探ってみてください。いずれも、すぐに見つかると思います）。

　・　背理法による有名な証明
　・　サイダックによる証明（この証明は非常に美しい…….）
　・　オイラーによる証明
　・　フェルマー数を用いた証明

(*3) 　\(\sqrt{2}\) が無理数であることの証明も４種類あり、割と分かり易いものもありますので、興味のある方はネットを探ってみてください。π が無理数であることの証明は少し難しいです（取り組み甲斐があるということもできますｗ）。

四方山話

この原稿を作成しているタイミングで、山口市が主催している（山口県、山口労働局が後援している）「やまぐち未来のしごとフェスタ」に参加していました。株式会社SYNCHROは「ホワイトハッカーを体験してみよう！」というテーマで「フィッシング詐欺」がどのように行われるのか？ をテーマにした出展を行いました（DNS reply を偽装することで偽サイトに誘導し、ID/パスワードを窃取するという実演を行いました）。来場してくださった中高生の皆さんが、サイバーセキュリティや、サイバーセキュリティ対策に少しでも興味を持って頂けたのであれば嬉しいです。お昼休みには、警察の方も説明を聞きにきてくださいました。こうして「理解」を拡げて行くことも大事なことだと思います。

フィッシング詐欺を行った場合に、どのような罪に問われるのか？　を改めて考えさせられました（質問されたらどう答えようというところから気づきです）。「フィッシング詐欺」という名称になっていますが、フィッシング詐欺をして個人情報を窃取する行為自体は、詐欺罪にも電子計算機使用詐欺罪にもなりません。では、問題はないのか？　というと、不正アクセス罪（不正アクセス禁止法違反）になります。そこで窃取した個人情報を利用してクレジットカードの不正利用を行った場合は、詐欺罪（10年以下の懲役）や電子計算機使用詐欺罪（10年以下の懲役）に問われる可能性があります。

流行のランサムウェア攻撃を行った場合は、「業務妨害罪」や、より重い「電子計算機損壊等業務妨害罪」に問われることになります。身代金を要求したり、身代金の授受に関与したりした場合には、「恐喝罪」や「犯罪収益等収受罪」などに問われる可能性があります。

ということで、攻撃の手段に通じている我々はダークサイドに堕ちないように（= 犯罪を犯さないように）「ホワイト」で在らねばならないということになります。

---

ＣＳ四方山話の過去の記事はこちら（合わせてお読みください）

サイバーセキュリティ四方山話の最新話は、メールマガジンにてもご案内致しています。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。