暗号を理解するための数学の世界　ＣＳ四方山話（第37話）

「小学校からの数学」シリーズ・第16弾です。前回に引き続き、小学５年生です。

5年生で学ぶ単純な図形の面積

５年生の算数では、三角形と四角形の面積を扱います。４年生で、正方形、長方形の面積を扱いましたが、５年生では、もう少し一般的な図形に発展させた形になります。

ここでは、４つの「公式」が登場します。

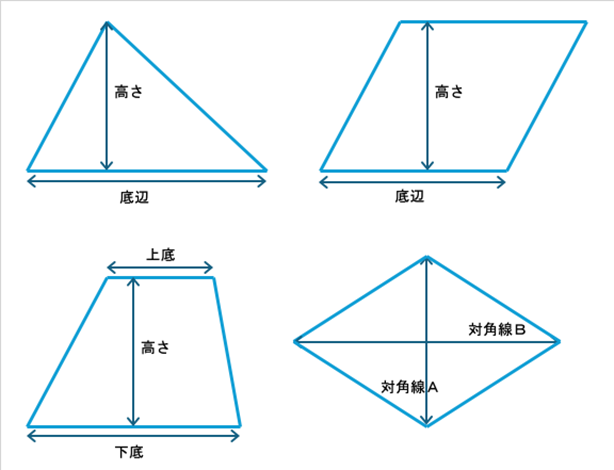
　・三角形の面積 ＝ 底辺 x 高さ ÷ 2
　・平行四辺形の面積 ＝ 底辺 × 高さ
　・台形の面積 ＝ ( 上底 ＋ 下底 ) × 高さ ÷ 2
　・ひし形の面積 ＝ 対角線Ａ × 対角線Ｂ ÷ 2

小学５年生の算数では、上記の単純な図形の面積のみを扱います。また、平面上の面積のみを扱います。

一般的な（数学における）面積としては、平面上、あるいは曲面上の面積になります。小学６年生では、立体の表面積（立体を構成するすべての面の面積を足し合わせたもの）が登場します。

中学校では、面積比を扱います。この段階では、平面上の図形で、かつ、辺が線分の図形に限定されています。また、円柱、円錐、球の表面積も登場します。

高校では、数Ⅱで定積分と面積の関係を扱います。平面上に限定されますが、一部の境界が関数で定義された曲線である場合も対象に広がります。数Ⅲでは関数で表現される複数の曲線で囲まれた領域の面積も扱います。

曲面積（曲面上の面積）は、大学で扱う範囲になります。

高校の数Ⅱにならないと「算数の面積」は「数学」と出会えません。ダメだなぁとは思うなかれ。

幾何学と代数学が出会うのには「歴史」と言うべき時間が掛かっています。古代ギリシャ（紀元前２世紀頃）でも、すでに図形を方程式で表現することが行われていました。面積や体積を x^2, x^3 を使った式で表したりしていました。しかし、「座標」や、曲線を代数方程式で記述するといったことは、フェルマー (1601-1665) の登場まで、1800年以上も待つ必要がありました。

円と多角形

これまでの小学校の課程では、図形としては、円、三角形、四角形しか登場していませんでした。

５年生で、正多角形も登場します。皆さまもご存知の通り「正多角形」とは「すべての辺の長さが等しく、かつ、すべての頂点の角度が等しい」多角形を指します。

また５年生では「円周率」が登場します。円周率 ＝ 円周 ÷ 直径 ですが、この値は「無理数」で分数では表現できません。一時期の日本では「円周率は 約3」と教えていたようですが、これだと円ではなく「正六角形」になってしまいます。現在（2024年度）では、円周率を「3.14」と教えているようです。実際の円周率は、2024年2月末時点で105兆桁まで算出されています。

円周率「π」は、数学上で最も重要な定数とされています。

２番目は、「ｅ」ネイピア数。自然対数の底で、微積分において最も重要な定数です。高校の数Ⅲで登場します。

πもｅも無理数であり、かつ超越数（代数的数でない複素数 = 有理係数の代数方程式の解にもならない複素数）です。

３番目は「γ」オイラーの定数（オイラー・マスケローニ定数とも呼ばれる）。γも超越数であると目されているが（未だに）無理数であるか有理数であるかも判明していません。数学上の未解決問題の１つです。(※1）

柱と円柱

小学５年生では、扱う立体図形も増えます。立方体、直方体、球だけだった世界に、多角柱と円柱も加わります。多角形も学んだところですので、多角柱も登場します。

多角柱の定義は「平行な2つの平面とそれらに交わる直線、およびその上の多角形によって囲まれた立体」です。小学５年生では、側面が底面に垂直な多角柱しか登場しない、つまり、斜多角柱は登場しないようです。

立体図形も増えたこともあって、立体図形の「面」「辺」「頂点」の数という概念も登場します。

まとめ

今回は、小学５年生の課程の「図形の面積」と「円と多角形」「角柱と円柱」を勉強しました。すべて図形のネタで、ネットワーク技術と関係の深い代数学の話題はあまり登場しませんでした。

さて次回（第38話）は、いよいよ小学校の最終学年である６年生に進級します。引き続き、ご購読頂ければ幸いです。

また、「ＣＳ四方山話」の電子書籍 第１段「サイバーセキュリティ四方山話 VOL.1」は、2024年10月1日に ConTenDo さんから発売になっております。こちらも、よろしくお願い致します。

https://contendo.jp/store/contendo/Product/Detail/Code/J0010582BK0159582001

第２段も鋭意執筆中です！　年末年始で完成させようと思っていましたが、まだ進行中です (^^;;

---

補足

(※1) 数学上の未解決問題

21世紀に入って四半世紀も経とうとしているんだから、未解決問題なんてもう残っていないんじゃないの？　と思うかも知れませんが、実際には多々あります。ザッと挙げても100ぐらいの未解決問題があります。

その未解決問題の中でも、主なモノ（数学全体に影響するモノ、科学や技術に多大な影響があるモノ）は「ミレニアム懸賞問題」と呼ばれ、米国のクレイ数学研究所が7つの問題に関して、2000年にそれぞれ US$1,000,000の懸賞金を掛けています。

• P≠NP予想
• ホッジ予想
• ポアンカレ予想
• リーマン予想
• ヤン-ミルズ方程式と質量ギャップ問題
• ナビエ-ストークス方程式の解の存在と滑らかさ
• BSD予想

この内、ポアンカレ予想に関しては解決済み。2002〜2003年にグリゴリー・ペレルマンがポアンカレ予想の証明に関する論文３件を発表。複数の数学者が検証した結果、証明は正しいと判定され、2010年にペレルマンは受賞した。しかし、ペレルマンは賞金を辞退しため、クレイ数学研究所が「数学界に貢献するために使う」とされている。

四方山話

2025年1月に連邦政府機関がIT業界に対して「Memory Safe」ではない言語（主にはC、C++）でのアプリケーション開発を中止すること、既存のアプリケーションを他言語へ移行するためのロードマップの策定を2026年1月1日までに作成することを要請しました。

C、C++ は（実装に深く関わったことがあるヒトは全員が体感していると思いますが）ある意味危険なプログラミング言語です。pointer という便利な機能があるお陰で、簡単に「buffer over run」したり、「memory leak」したりする処理を書くことが「可能」です。また、関数ポインタという攻撃者にとっては、とても美味しい情報が変数として授受できたりもします。

心無い programmer が書いた code は、どんなことが起こるか分からないびっくり箱のようなモノですし、心有る programmer が注意深く書いても、尻尾を捕まえられない不可解な現象を発生することがあります。こうしたプログラミング言語の特性は、多くの脆弱性を発生させることになりますし、codeを静的に眺めても、その脆弱性の把握は困難ということに繋がります。

安全な世の中にするため、プログラミング言語をC、C++から、Memory SafeなGo、Rust、Swift、C#、Python、Java などに移行することを進めて行くことになるでしょう。長年（人生の半分以上）、C、C++ に関わって来た我が身としては、一抹の寂しさも感じています。

雑談

この冬は全国的に降雪が多くご苦労されている方もおられると思いますが、山口市のオフィスや自宅のあるエリアは、今年に入って何度か積雪がありました。子供の頃は「雪」は「嬉しい」「楽しい」に繋がっていましたが、大人になってからは道路が渋滞する、公共交通機関が遅れるなど「不安」「面倒」に繋がってしまうことが悲しいですね。それだけ時間に追われて生活していることを改めて認識させられます。だって、時間を気にせず、暖かい部屋の窓から降る雪を眺めたり、暖かい格好をして近所を散策するのであれば、それは「ワクワク」に繋がりますから。

---

Ｓ四方山話の過去の記事はこちら（合わせてお読みください）

サイバーセキュリティ四方山話の最新話は、メールマガジンにてもご案内致しています。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。