暗号を理解するための数学の世界　ＣＳ四方山話（第38話）

「小学校からの数学」シリーズ・第17弾です。前回予告の通り、今回から小学校からの最終学年、小学６年生です。今回は「分数」について扱います。

小学校の算数での「分数」

最終学年ですので、小学校の算数での分数について振り返りましょう。分数の概念と表記は古代エジプト(※1) で登場しますが、小学校の算数では、分数は２年生で初登場します。そして、毎学年で登場します。ざっとまとめると次の通りです。

• ２年生：分数の概念、簡単な分数（1/2, 1/4など）
  • ちなみに、この簡単な分数、つまり分子が「１」の分数、つまり単位分数は、古代エジプトで登場する分数と同じです。
• ３年生：分数の基礎（割り算、小数点、分数など）
• ４年生：通分
• ５年生：約分

そして６年生では、分数のかけ算、分数のわり算が登場します。

分数のかけ算

いくつかのパターンに分けます（小学校でもそのように教えているようですので）。

分数 × 整数：

3 7 × 4 ＝ 12 7 ← 分子に整数を掛けるだけのパターン

3 8 × 4 ＝ 3 2 ← 分子に整数を掛けて、約分するパターン

3 8 × 16 ＝ 6 ← 分子に整数を掛けて、約分し、結果が整数になるパターン

分数 × 分数：

3 7 × 4 5 ＝ 12 35 ← 分子・分母をそれぞれ掛けるだけのパターン

3 8 × 4 5 ＝ 3 10 ← 分子・分母をそれぞれ掛けて、約分するパターン

3 8 × 16 3 ＝ 3 ← 分子・分母をそれぞれ掛けて、約分し、結果が整数になるパターン

帯分数 × 整数：

1 3 7 × 4 ＝ 10 7 × 4 ＝ 40 7 ＝ 5 5 7 ← 分子に整数を掛けるだけのパターン

1 3 8 × 4 ＝ 11 8 × 4 ＝ 11 2 ＝ 5 1 2 ← 分子に整数を掛けて、約分するパターン

1 3 8 × 16 ＝ 11 8 × 16 ＝ 22 ← 分子に整数を掛けて、約分し、結果が整数になるパターン

分数 × 小数：

3 7 × 0.4 ＝ 3 7 × 4 10 ＝ 3 7 × 2 5 ＝ 6 35 ← 分子に小数を掛けるだけのパターン

3 8 × 0.4 ＝ 3 8 × 4 10 ＝ 3 8 × 2 5 ＝ 3 20 ← 分子に小数を掛けて、約分するパターン

3 8 × 1.6 ＝ 3 8 × 16 10 ＝ 3 8 × 8 5 ＝ 3 5 ＝ 6 10 ＝ 0.6 ← 分子に小数を掛けて、約分し、結果を小数にするパターン

分子、分母に分かれていますが、基本的にそれぞれが整数の計算で、そこに（分子、分母共通の約数を消す）約分という操作が加わるということです。

帯分数も、小数も、真分数（分子が分母より小さい分数）か仮分数（分子が分母と等しいか、分子が分母より大きい分数）に変換すれば、上記の手順に持ち込めるので同じことです。

分数のわり算

分子のわり算は「割る分数の分子・分母を逆にする」という操作が加わるだけで、そこから先はかけ算と同じです。

「割る分数の分子・分母を逆にする」の意味は、以下の通りです。

数値 ÷ 分子/分母 = 数値 ÷ ( 分子 ÷ 分母 ) = 数値 ÷ 分子 x 分母 = 数値 x ( 分母 ÷ 分子 ) = 数値 x 分母/分子 　かけ算のときと同じように、パターン分けしましょう。

分数 ÷ 整数：

3 7 ÷ 4 ＝ 3 28 ← 分母に整数を掛けるだけのパターン

3 8 ÷ 6 ＝ 1 16 ← 分母に整数を掛けて、約分するパターン

分数 ÷ 分数：

3 7 ÷ 5 4 ＝ 3 7 × 4 5 ＝ 12 35 ← 割る分数の分子・分母を逆にして、分子・分母をそれぞれ掛けるだけのパターン

3 8 ÷ 5 4 ＝ 3 8 × 4 5 ＝ 3 10 ← 割る分数の分子・分母を逆にして、分子・分母をそれぞれ掛けて、約分するパターン

3 8 ÷ 3 16 ＝ 3 8 × 16 3 ＝ 2 ← 割る分数の分子・分母を逆にして、分子・分母をそれぞれ掛けて、約分し、結果が整数になるパターン

帯分数 ÷ 整数：

4 3 5 ÷ 3 ＝ 23 5 ÷ 3 ＝ 23 15 ＝ 1 8 15 ← 割る分数の分子・分母を逆にして、分母に整数を掛けるだけのパターン

2 5 8 ÷ 3 ＝ 21 8 ÷ 3 ＝ 7 8 ← 割る分数の分子・分母を逆にして、分母に整数を掛けて、約分するパターン

分数 ÷ 小数：

3 2 3 ÷ 0.3 ＝ 11 3 ÷ 3 10 ＝ 11 3 × 10 3 ＝ 110 9 ＝ 12 2 9 ← 割る分数の分子・分母を逆にして、分母に小数を掛けるだけのパターン

2 3 5 ÷ 0.3 ＝ 13 5 ÷ 3 10 ＝ 13 5 × 10 3 ＝ 26 3 ＝ 8 2 3 ← 割る分数の分子・分母を逆にして、分母に小数を掛けて、約分するパターン

4 1 5 ÷ 0.3 ＝ 21 5 ÷ 3 10 ＝ 21 5 × 10 3 ＝ 7 × 2 ＝ 14 ← 割る分数の分子・分母を逆にして、分子に整数を掛けて、約分し、結果が整数になるパターン

分数の比較

分数同士の比較という課題も、小学6年生で登場します。

　「 と  とどちらが大きいでしょう？」という問題です。

皆さんはどうするでしょうか？　目の前に電卓があれば..。最近、物理の電卓を見かける機会は減りましたね。言い換えますと..。スマートフォンやPCの電卓アプリが目の前にあれば、計算してみますよね？　筆者であればそうします。というか、そうしました。

2 3 ≒ 0.6666666…

11 17 ≒ 0.6470588…

2 3 > 11 17 ということですね。

小学校の学習では、分数同士の比較で行います。分母を同じにする「通分」ということですね。

2 3 = 34 51 > 33 51 = 11 17

まとめ

今回は、小学６年生の課程で登場する「分数」に関して取り上げました。さて次回（第39話）は「並べ方と組み合わせ方」に関して学びます。小学６年生で「順列組合せ」が登場するのですね。引き続き、ご購読頂ければ幸いです。

また、「ＣＳ四方山話」の電子書籍 第１段「サイバーセキュリティ四方山話 VOL.1」は、2024年10月1日に ConTenDo さんから発売になっております。こちらも、よろしくお願い致します。

https://contendo.jp/store/contendo/Product/Detail/Code/J0010582BK0159582001

　 第２段も鋭意執筆中です！まだ進行中です (^^;; 　進捗が捗々しくなくてスミマセン..。

---

補足

(※1) 古代エジプトの分数
古代エジプトの「神聖文字（ヒエログリフ）」では、基本的には単位分数を使います。数字の上に「目」ような形状の記号を置くと、それは単位分数になります。1/2 と 2/3 だけは例外で、特別なグリフがあります。図は、筆者が手書きしたものですので、雑な部分はご容赦ください。

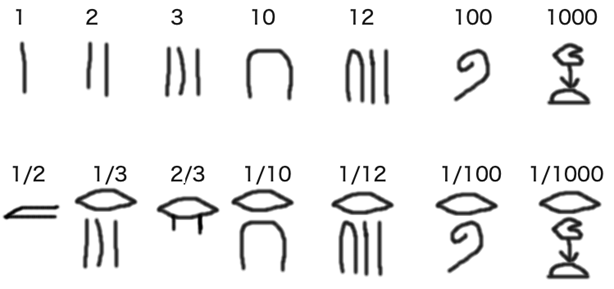
分母が異なる単位分数の和を「エジプト分数」と呼びます。

さまざまな分数は、エジプト分数で表すことが可能です。 例えば、下記の通りです。

6 7 = 1 2 + 1 3 + 1 42

数学的な表現をすると「任意の有理数は単位分数の和で表せる」ということになります。

　証明としては「調和級数が発散する」ことを利用するのですが、ここで詳説すると長くなりますし、小学校の範囲を大幅に逸脱しますので、証明は省略させて頂きます。

---

雑談

この「雑談」を第38話の仕上げとして、執筆しているのは４月上旬です。桜の季節もそろそろ終わりです。それは名残惜しいのですが、個人的に今年は花粉症が辛かったので、その時期がもう少しで終わると思うと明るい気分になります。初夏から夏に、いくつか楽しみなイベントも待っていますし。

５月には、山口のサイバーセキュリティ対策センター（CSCC）恒例の「春BBQ」があります。CSCCのメンバは５月で30名を超えるので、より盛大になるでしょう。６月には、湯田温泉こんこんパーク」（https://www.konkon-park.com/）がオープンします。単なる温浴施設ではなく、全天候型の大屋根広場、多目的スペース、デッキスペース、芝生広場・噴水広場などもあります。筆者の（山口の）自宅から徒歩２分という点も個人的なメリットです。

そして、８月には、CSCCとしての大きなイベントを開催します。この件に関しては「ＣＳ四方山話」でも、今後ご案内して行きます。お楽しみに！

---

サイバーセキュリティ四方山話の過去の記事はこちら（合わせてお読みください）

サイバーセキュリティ四方山話の最新話は、メールマガジンにてもご案内致しています。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。