白狐村塾（第３話）
基礎から徹底解説！　ストリーム暗号とは何か？　RC4から、Salsa20、ChaCha20まで

前回は、楕円曲線暗号までで（編集さんにご迷惑をお掛けしない）丁度良い長さになりました。結果、前回書き切れなかった「ストリーム暗号」について書きたいと思います。なかなか予告通りに進行しなくてスミマセン。「四方山話」から読んでくださっている方々は「ああ、またか」と流してくださるのでは？ という甘えもありますが、気を付けようとは思っています。

共通鍵暗号方式 vs 公開鍵暗号方式

一部「おさらい」（復習）ということになりますが、暗号方式を俯瞰してみましょう。方式に関しての大きな分類としては２つあります。

１つは「共通鍵暗号方式、公開鍵暗号方式」です。共通鍵暗号方式では、暗号化も復号化も同じ鍵で行います。皆さんが、ファイルを暗号化する時に使うzipやLHAはこの暗号化方式を使っています。掛けた鍵で開けられるということで、分かり易いですね。

公開鍵暗号方式では、秘密鍵と公開鍵の２つの鍵を使います。この２つはペアです。公開鍵で暗号化したものは、そのペアの秘密鍵で復号化することができます。公開鍵で暗号化したデータを公開鍵で復号化することはできません。この特性を利用して、署名や認証といった機能を実現することが可能です。
表にまとめると、次のようになります。

ECDSAは楕円曲線暗号です（厳密に言えば、楕円曲線を用いた署名アルゴリズムです）。EdDSAはエドワーズ曲線を用いた暗号（署名アルゴリズムです）。エドワーズ曲線は、楕円曲線の一種ですので、どちらも、広義の「楕円曲線暗号」ということもできます。

ＣＳ白虎村塾・第１話のRSA暗号も、第２話の楕円曲線暗号も公開鍵暗号方式の仲間です。

ブロック暗号とストリーム暗号の違いは？

さて、もう１つの大きな分類は「ブロック暗号、ストリーム暗号」です。前回の「楕円」も今回の「ストリーム」も、その字面だけでは何のことだか分かりませんよね。「楕円」は余程のマニアでなければ意味が分かりません。しかし、第２話を読んでくださった皆さまは「楕円」にもすっかり馴染んで頂いたのでは？ と思います（ホント？？）がいかがでしょうか？

ブロック暗号というのは、暗号化したいデータを決まったサイズに分割して、その分割したサイズごとに平文から暗号文に変換する方法です。暗号を解く場合も、同様にブロック単位で処理します。これに対して、ストリーム暗号というのは、入力されたデータを逐次（通常は１byteずつ）平文から暗号文に変換していくという方法です。暗号を解く場合も同様に逐次処理します。

データファイルのように全部のデータが揃っている場合はどちらでも大差ありませんが、通信の場合は、ストリーム暗号を使う場合が多いです。ブロック暗号の場合は、そのブロックサイズになるまでデータを溜めてから処理する必要があります。これに対してストリーム暗号は、入ってきたデータを逐次処理できるので処理効率を上げやすく、データを溜める必要がないので遅延が小さくなるメリットがあります。

表にまとめると、次のようになります。

お馴染みのRSA暗号も楕円曲線暗号もブロック暗号です。ではストリーム暗号は？　というのが今回の主題なのですが、もう少し細分化すると次表のようになります。

この表の中身を説明しましょう。暗号方式には「安全」であることが必須なのですが、並列処理が可能で、ランダムアクセスが可能（好きなところだけ読める）という「便利」さも要求されます。

ECB (Electronic Code Book) mode は「便利」なのですが、同じ平文のブロックは同じ暗号文のブロックに変換されます。このため解析が容易で「安全ではない」ということになり、この方式は使われていません。

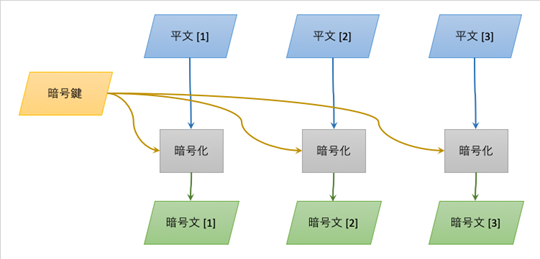
CBC (Cipher Block Chaining) mode では、１つ前のブロックの暗号文と、当該ブロックの平文とのXORをとったものを暗号化したものが暗号文になります。これを繰り返して行きます。この処理によって、ECBの欠点を補います。最初の平文は相手が居ないので、「初期化ベクトル」というブロックを用意しておき処理します。

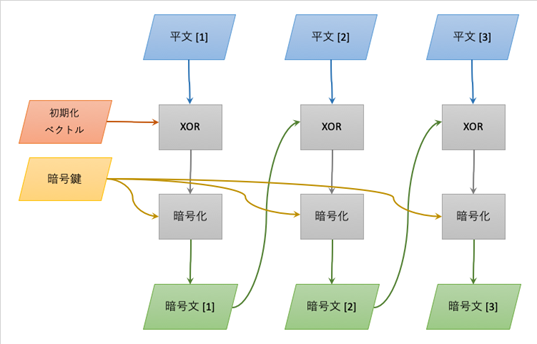
ただし常に前のブロックの暗号化の結果が必要になるので、暗号化の処理を並列で行うことはできません。

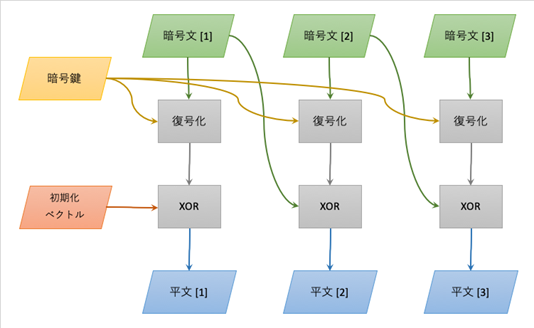
復号化も同様に初期化ベクトルが必要です。ただし、これは１つ目のブロックの復号化のみで、連続する２つの暗号文のブロックから平文のブロック１つを作れることから、並列処理やランダムアクセスが可能です。

ストリーム暗号にもいくつかのモードがありますが、先ほどの表でみると一目瞭然で、CTR ( Counter ) mode が一番「便利」です。結果、主要なストリーム暗号はCTR mode です。ここで「Counterって何？　何をカウントするの？」という質問になろうかと思いますが、その答えは「内部状態を記述するカウンタ」ということになります。それでは、ストリーム暗号を詳しく見ていきましょう。

ＲＣ４

具体例があった方が良いので、ここでは「RC４」を挙げます。RC4は、米国のRonald Rivestさんが1987年に設計したストリーム暗号です。当初は公開されない方式でしたが、1994年に誰かがメーリングリストでRC4の解説記事を流してしまったので、衆人の知るところとなりました。

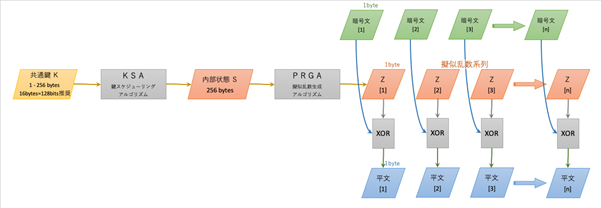
処理方法を簡単に説明すると、鍵とKSA（Key Scheduling Algorithm）という処理によって、内部状態のテーブルを作ります。この内部状態を一定のロジックで変更しながら、PRGA（Pseudo-Random number Generate Algorithm）という処理によって、キーストリームを生成します。このキーストリームが真性乱数であれば解読困難になるわけですが、ロジックで生成した数列なので擬似乱数です。 暗号化の処理自体はシンプルで、入力された平文のストリームと、キーストリームとのXORを暗号文のストリームとして出力するだけです。同じ「鍵」からは必ず同じキーストリームが生成されるので、暗号化時の「鍵」を使えば復号化できるということになります。つまり共通鍵暗号方式ということです。

RC4は容易に実装可能なので、WiFiで用いられるWEP、WPAや、TLS/SSL、SSHなど、さまざまなモノに適用されました。しかし広く使われると言うことは攻撃の対象にもなりやすく、コンピュータの演算能力が飛躍的に向上した2015年頃には、RC4で暗号化された（Webブラウザで使用される）cookieが52時間で解読できたといった報告が上がるようになりました。内部状態復元攻撃、鍵回復攻撃、平文回復攻撃など多くの攻撃方法が提示されています。IETFが非推奨とするRFCを公開する(*1)などもあり、 2016年にはChromeやFirefoxなどのブラウザも使用を止め、過去の技術になりました。 ただ、ストリーム暗号の土台となった技術ですし、前述の通り実装し易いので、ストリーム暗号を学ぶには良い題材です。ということで、RC4のコード（Ｃ言語のソースコード）を示します。このコードはNICTさんの情報などを参考に、筆者が30分でcoding、30分で動作確認と修正を行った雑なモノなので「キツイ、ツッコミ」はご遠慮ください。処理のフローについては後述します。

---

#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#define N 256

// Key Scheduling Algorithm
int KSA(unsigned char *ucKey, unsigned char *S)
{
    int i = 0, j = 0;
    unsigned char ucTmp = 0;

    // initialize S[]
    for (i = 0; i < N; i++)
        S[i] = i;
    
    // KSA setup
    int iLen = (int)strlen((char *)ucKey);
    for (i = 0; i < N; i++) {
        j = (j + S[i] + ucKey[i % iLen]) % N;
        ucTmp = S[i];
        S[i] = S[j];
        S[j] = ucTmp;
    }

    return 0;
}

// Pseudo-Random number Gemnarate Algorithm
int PRGA(unsigned char *S, unsigned char *ucIn, unsigned char *ucOut)
{

    int i = 0, j = 0;
    unsigned char ucTmp = 0;

    for (size_t n = 0, iLen = strlen((char *)ucIn); n < iLen; n++) {
        i = (i + 1) % N;
        j = (j + S[i]) % N;
        unsigned char ucKey = S[(S[i] + S[j]) % N];
        ucTmp = S[i];
        S[i] = S[j];
        S[j] = ucTmp;
        ucOut[n] = ucKey ^ ucIn[n];
    }

    return 0;
}

// Ronald Rivest 4 encryption
int RC4(unsigned char *ucKey, unsigned char *ucIn, unsigned char *ucOut)
{
    unsigned char S[N];

    KSA(ucKey, S);
    PRGA(S, ucIn, ucOut);
    return 0;
}

// RC4 sample main routine
int main(int argc, char *argv[])
{
    printf("RC4 Program\n");
    if ( 2 > argc ) {
       printf("  [Error] usage: rc4 <Key string> <input text>\n");
       return -1;
    }

    unsigned char *ucKey = (unsigned char *)argv[1];
    unsigned char *ucIn  = (unsigned char *)argv[2];
    printf("Input     text: %s\n", (char *)ucIn);
    size_t size = sizeof(char) * strlen((char *)ucIn);

    unsigned char *ucOut = calloc(size + 1, sizeof(unsigned char));
    RC4( ucKey, ucIn, ucOut );

    printf("Encrypted text: ");
    for (size_t i = 0; i < size; i++)
        printf("%02hhX", (char)ucOut[i]);
    printf("\n");

    unsigned char *ucDec = (unsigned char *)calloc(size + 1, sizeof(unsigned char));
    RC4( ucKey, ucOut, ucDec );

    printf("Decrypted text: ");
    for (size_t i = 0; i < size; i++)
        printf("%c", (char)ucDec[i]);
    printf("\n");

    free( ucOut );
    free( ucDec );

    return 0;
}

---

書いたコードを試すためのmain()関数を除くと、RC4 の処理自体は「56行」で書けます（もっと短くもできますが）。お手軽ですね。 作ったこのプロフラムを実行してみると、下記のようになります。

---

$ ./rc4 "KATABAMI ZTNA Environment" "パパッとコーディング"
RC4 Program
Input     text: パパッとコーディング
Encrypted text: A239075E382B8D52744C3C2A5853FC9D9889DB0C3FCD5975F7C332D4E4C4
Decrypted text: パパッとコーディング

---

　”KATABAMI ZTNA Environment”が「鍵」で、”パパッとコーディング”をこの鍵を使って暗号化したものが “A2390..” です（16進数表記です）。同じ鍵で復号化すると元の文字列になりました。メデタシ、メデタシ。

処理内容を図で表すと次のようになります。

暗号化処理：

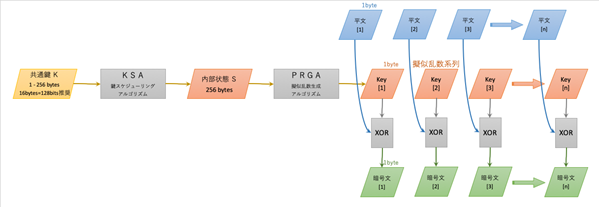
復号化処理：

Salsa20、ChaCha20、ChaCha20-Poly1305

現在、多用されているストリーム暗号は、認証付き暗号（AEAD = Authenticated Encryption with Associated Data）である「ChaCha20-Poly1305」です。RC4以降、色々なストリーム暗号、擬似乱数生成方式が登場しましたが、大人的ないきさつ (*2)  があり、「ChaCha20-Poly1305」に行き着いています。具体的な仕様はRFC 7539をご参照ください (*3)。

「ChaCha20」がストリーム暗号で、「Poly1305」はメッセージ認証(MAC = Message Authentication Code) になります。その「ChaCha20」の元になっているのが「Salsa20」です。 Salsa20は、数学者・暗号学者であるDaniel Bernsteinさんが2005年に設計したストリーム暗号で、パブリックドメインとして公開されています。内部状態は、4 x 4 の 32bits整数の行列で記述されます。この内部状態を次のような演算でかき混ぜながら、鍵ストリーム（擬似乱数列）を生成します。

a += b; d ^= a; d <<<= 16;
c += d; b ^= c; b <<<= 12;
a += b; d ^= a; d <<<= 8;
c += d; b ^= c; b <<<= 7;

初期の内部状態は次の通りです。処理の詳細はWikiにもC/C++のソースコードが記載されているので参考にしてください。(*4)

ChaCha20は、Salsa20の処理パフォーマンスを向上したもので、Bernsteinさんが2008年に発表しました。内部状態の記述方法はSalsa20と同じですが、初期状態の並びが変わっています。こちらも、処理の詳細はWikiにもC/C++のソースコードが記載されているので参考にしてください。(*4)

ちなみに、SYNCHROの「KATABAMI」では、Salsa20の改良版であるXSalsa20とPoly1305を組合せたストリーム暗号をペイロード（エンドポイント間で授受されるデータ）の通信に用いています。

RC4とSalsaの系列を整理すると次のようになります。

まとめ

今回はストリーム暗号について書きました。ザックリと言えば「鍵」を使って再現可能な擬似乱数を使って「鍵ストリーム」を生成して、その「鍵ストリーム」と「入力ストリーム」のXORで「暗号化ストリーム」を生成するのがストリーム暗号ということになります。 さて次回ですが、実は第２話を書いているときから決まっています。暗号化方式から少し離れて、暗号や通信を扱う上で「知ってもらいたいこと」と「教育」という（少し捻った）視点で書いてみようと思います。ということで、次回もお楽しみに！

---

(*1) RFC7465 “Prohibiting RC4 Cipher Suites”
https://datatracker.ietf.org/doc/html/rfc7465

(*2) Dual_EC_DRBG BackDoor

詳しく解説すると、この件のみで充分１話になってしまうので、端折って説明します（詳しくは、https://techmedia-think.hatenablog.com/entry/2020/10/14/235117 などをご参照ください）。

Dual_EC_DRBG という楕円曲線を使った乱数生成器が提案され、2006年にNIST SP800-90Aで採用されました。2013年に、内部告発によってバックドアが仕掛けられていることが判明しました。国家による関与（監視）と個人の自由とのせめぎ合い、NIST vs IETF という、興味深い図式です。IETF（Internet Engineering Task Force）は、RFCを取り纏めている団体なので「ＣＳ四方山話」「ＣＳ白狐村塾」にも度々登場しますので、覚えてください。そのIETFの押しは、NISTで採用されていない「Ed25519」や「ChaCha20-Poly1305」です。

(*3) RFC 7539 “ChaCha20 and Poly1305 for IETF Protocols”
https://datatracker.ietf.org/doc/html/rfc8439

(*4) Sals20 on Wiki　https://ja.wikipedia.org/wiki/Salsa20

---

白狐村塾話の過去の記事はこちら（合わせてお読みください）
ＣＳ白狐村塾（第１話）サイバーセキュリティに必須の技術、詳細に解説！　その1
ＣＳ白狐村塾（第１話）サイバーセキュリティに必須の技術、詳細に解説！　その2
ＣＳ白狐村塾（第２話）楕円曲線暗号について

サイバーセキュリティ白狐村塾は、新たなお話が公開されたときにメールマガジンにてご案内致します。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。