白狐村塾(第5話)「群・環・体」の群、四元論と圏論を分かりやすい実例から学ぼう!
白狐村塾では、第4話から数学の世界、「数論」に踏み込んできましたが、このテーマは今回で締めますので、もう少しお付き合いください。さて今回は「群・環・体」の内「群」を取り上げて「何に使えるのか?」の例をご説明したいと思います。また、折角ここまで来ましたので、実用性が高い「四元数(しげんすう)」と「圏論(けんろん)」についてもお話しできればと思います。
パズルやコインの状態から「群」を学ぼう
「群」に関しては、CS白狐村塾・第2話で、楕円曲線を説明する際に触れさせて頂きました。
おさらい(復習)になりますが、「群」の定義は以下の通りです。
集合をGとします。(二項)演算を🔺と定義します。
1) 集合Gに含まれる ある要素 e と任意の要素 g に関して、下記が成り立つ
e▲g=g▲e=g
2) 集合Gに含まれる ある要素 h と任意の要素 g に関して、下記が成り立つ
h▲g=g▲h=e
3) 演算🔺に関して、常に結合法則が成り立つ
結合法則とは、下記が成り立つことです(これは私でも知っていました)。
(a▲b)▲c =a▲(b▲c)
さらに、下記の条件も充足する場合、群 (G, ▲) は「可換群(アーベル群)」と呼ばれます。
4) 演算🔺に関して、常に交換法則が成り立つ
交換法則とは、下記が成り立つことです(これも私でも分かります!)。
a▲b =b▲a
それでなんなの? 何に使えるの? 良く分からない。単位さえ取れればいいや。
若かりし私は、そういう浅薄な思考経路で、群論を理解しようとしませんでした。
私の中での結論としては、「当時、群・環・体を習得できなかった私。しかし、それは私の問題ではなく、指導方法の問題」です。もちろん言い訳? 責任転嫁? の部分もありますが、私の主張を支えてくれる素晴らしいドキュメントを見つけました!!
「群論概念の知的必要性を生じさせる指導デザイン」です。(*1) 濱中先生、大滝先生、袴田先生に本当に感謝です。
私がここで説明するよりも、原本を参照して頂いた方が良いと思いますが、私なりの理解を書いておきます。
➣普通のヒトは、数には日常でも慣れ親しんでいるが、代数構造体なんて知らない。
➣人間行動学では知的活動は「実践」と「理論」とに分けられる。実践はタスクとテクニック、理論はテクノロジとセオリ。いきなり「理論」を説くのではなく、「実践」の中で「セオリ」を見つけさせ、そこから「理論」に導くのが「教育」
➣高校までの教育では、ベクトルも含め計算の仕方を教える。これは実践。しかし、大学の線形代数では、計算方法ではなく「性質」を教えようとする。これは理論。そこに「分かりづらさ」がある。
➣群・環・体の中で「群」の性質から教えようとするが、順番はそれで良いのだろうか?
ということで、先生達は「パズル」という課題=実践から理論に導く方法を採っています。これは、非常に有効だと思います(詳しくは、原本をご参照ください)。
もう1つ例を挙げておきます。
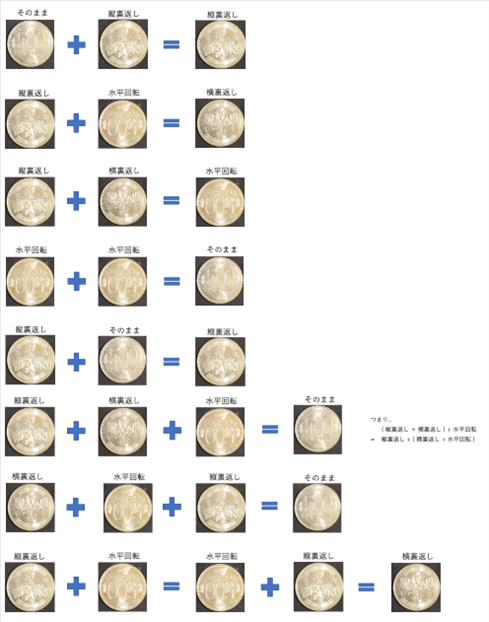
机の上に置いたコインを考えてみます。180度以外の回転は考えないことにします(水平面内での回転は180度のみとします。机の上に置くことで、自ずと残り2自由度の回転は180度に限定されます)。
それぞれの状態(= 値)で思い付くモノを挙げましょう。「縦裏返し」「横裏返し」「水平回転」の3つが思い付きますね。忘れてはいけないのは、元の状態。それは「そのまま」としましょう。4つの状態(= 値)が定義されました。

次に2つの値を使った 演算 = 加法 を考えます。
「そのまま」の状態に「縦裏返し」を足すは、「そのまま」の状態に「縦裏返し」を行うとします。結果は「縦裏返し」の状態になります。
「縦裏返し」に「横裏返し」を足すと「水平回転」、「水平回転」に「水平回転」を足すと「そのまま」となります(全部は挙げませんので試してみて下さい)。
どの加法(足し算)を行っても4種類のいずれかの状態になります。つまり「閉じている」ということになります。
「そのまま」が「単位元」です。
「水平回転」の逆元は「水平回転」。他も同じで、自分自身が「逆元」になります。
そして、結合則も成り立ちます。また、交換則も成り立ちます。
ということは、このコインの例は「群」であり「アーベル群(可換群)」ということになります。 「なんだ、簡単じゃない!」そう思って頂ければ嬉しいです。
同様に、いわゆる「15パズル」も「ルービックキューブ」も群であり、群論で解くことが可能です。(*2)。群論はパズルを解くためのものではありませんが、分かり易い実例として挙げておきます。
ここで、「群・環・体 」と「数」との関係も示しておきましょう。
「整数」は「環」であり、乗法に関しての単位元を持つ「可換環」ということになります。 有理数、実数、複素数は「体」ということになります。
3次元の物体の記述に便利な四元数(しげんすう)
「群・環・体 」とは少し位置付けが異なりますが、四元数 = クォータニオン (Quaternion) という概念もあります。
これは複素数の拡張ですね。あるいは、複素平面を3次元に拡張したものとも言えます。高校数学で実数→複素数と,数を扱う範囲が広がりましたが,さらに複素数をパワーアップしたのが四元数です。
具体的には a+bi+cj+dk で表せる「数」でa,b,c,d は 実数で i2=j2=k2=ijk=-1 です。
これは比較的新しい概念で、1843年にウィリアム・ハミルトンが広めたものです。(*3)
もちろん数学的な意味もあるわけですが、3次元の物体を記述するのに便利で、剛体の回転運動や、結晶構造の解析などに役立ちますし、3次元グラフィックスなど3次元での回転を扱う場面で利用されています。3次元での物体の扱い(移動、回転、拡大・縮小)にはアフィン変換行列(回転だけであれば、3x3の回転行列)を使う場合も多いです(筆者がその昔、3次元のサーフェィスモデルやソリッドモデラを扱っていた時には、アフィン変換行列と格闘していました)。
四元数は、こうした行列と比較すると、よりコンパクトに表現できるという計算機的なメリットもあります。ここでは、四元数の使い方までは説明しませんが、こんな「数」の概念もあるのだということも知って頂ければと思い、取り上げさせて頂きました。
数学的な構造と集合の関係性を扱う圏論(けんろん)
群論、可換環論、体論などに加えて、まだ50年と歴史が浅いですが「圏論」という概念があります。計算機科学とも深く関連する概念です。特に、プログラミングをする方々にとっては、知っているとメリットがあると思いますし、理解しやすいと思うので、ここでも少し触れておきたいと思います。
いままでお話ししてきたとおり、ヒトは、自然数、整数、有理数、実数、複素数、四元数 と数の概念を拡張してきました。また、構造を持った集合としての 群・環・体 という概念も導入してきました。さらに数学的な構造と集合を定義し、その間の関係性を扱おうとする概念が「圏論」です。あえて極端な表現を採れば、特定の対象(たとえば群)の閉じた世界を対象とするのではなく、対象間(たとえば群と群)の関係を扱おうということになります。
圏論では、物事を「対象」(Object)と「射」(Allow)で表現します。(*4)
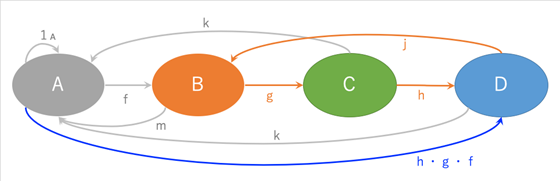
これって「状態遷移図(ステートマシン図)」じゃないの? と、プログラミングを体系的に学んだり、少し複雑なシステムの設計をされて、状態遷移図を書いたり眺めたりした皆さんは思うでしょう。
Cyberの世界の土台になっているコンピュータ(計算機)は、その名前の通り計算を行う装置です。では、計算とは何か? というとそれは、状態の遷移に他なりません。メモリ上に並べたビットの状態が変化することが「計算」なのですから。
ただ、プログラムのソースコードを書くヒト(=プログラマ)も、少なくともイマドキはメモリ上位置(番地)とか、その値(0 or 1)を意識したりはしません。もう少し抽象化した「状態」を定義して、その状態の遷移を記述することがプログラミングということになる訳です。
より抽象化の度合いを上げていくと、下記のような自然言語になります。これって、仕様の定義であり、要求仕様ということができます。
・ エアコンには、停止/暖房運転/除湿運転/冷房運転という4つの状態があります。
・ そして、エアコンには2つのスイッチがあります。
・ 停止状態で「1」というボタンを押すと、エアコンが起動して暖房運転を開始します。
・ その状態で「2」のボタンを押すと、エアコンは除湿運転になります。
・ その状態で「1」のボタンを押すと、エアコンは停止します。
・ その状態で「2」のボタンを押すと、エアコンは冷房運転になります。
・ その状態で「1」のボタンを押すと、エアコンは停止します。
:
だらだらと文章を並べると見通しが悪いので、これを図にします。
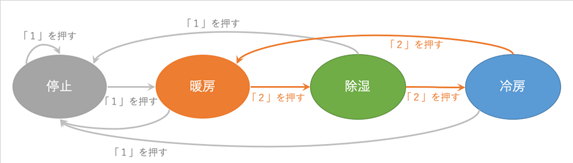
見慣れた? 状態遷移図になりましたね。これを、抽象化(一般化)すると1つ前のような図になります。
圏論では、下記の定義となります。
・1A というのは「対象A」の「恒等射」ということになります・隣り合った射は合成可能で、f、g、hの合成は「h・g・f」と記述します
・射の合成は結合則を満たします。(h・g)・f=h・(g・f)
・恒等射は、射の合成において単位元となります。f・1A=f
表現が数学的になってきましたが、ザックリ言うとこういう表現形が圏論の世界です。
こうした 対象、射 で描く図は、プログラムやシステム全体の把握に役立ちますし、状態遷移の抜け・漏れの検出にも役立ちます。
「対象」はプログラムでは「型」ということになります。プログラムに馴染んでいる皆さんは「型」という概念にはピンと来ますよね? int、char、float などの基本型もありますし、たとえばC言語であれば「構造体」(structure)というものがあり、struct { int iA; char cB; float fC; } というように、基本型を組み合わせて新たな型を定義することも可能です。数論における「数」も「複素数 ( a+bi )」や「四元数 ( a+bi+cj+dk )」のように複数の数の組合せで表現される数もあります。
「射」はプログラムでは「関数」ということになります。「システムコール」というシンプルな標準関数が存在し、それを組み合わせてもう少し複雑な関数を定義することが可能です。また、それらの関数を組み合わせて、より複雑な関数を定義することも可能です。
こうした積み重ねによって大規模なシステムを構築していくことになります。システムが大規模になっていくと、綻びも増えてくることになります。
対象と射をセットにして適用可能な射を明示的に限定する、そうした方向を採ったのが、C++やJavaに代表されるオブジェクト指向プログラミング言語です。プログラミング言語の系譜を図にすると次のようになります。

少し横道にそれますが、Webの普及によって、サーバ側で手軽に(インタプリタ)、軽快に動作するスクリプト言語として登場してきたのがPython、Ruby、JavaScriptなどです。
そして、今回の圏論とも関わりが深い、静的型付き、型推論、関数型プログラミングなどの特徴を持ったRust、Swift、Go、Ktolinなどが2010年代に登場してきました。これらは、1990年に登場したHaskellの影響を受けていると言われています。
型を明確に定義して使うことは、大規模なシステムをキチンと(不具合無く)動作させることに貢献します。
プログラマ向けのコメントになりますが、たとえば、C/C++は型の扱いには曖昧な部分があります(まあ、自由度があるという考え方もできるのですが)。ポインタ( * )というメモリの位置を指し示す型があり、これをシフトして(ずらして)参照することで、バッファなどの配列を手軽に&高速に扱うことができたり、void * という感じで元の型がないポインタを定義できたり、int ** のようにポインタのポインタも定義できたり、いろいろと便利です。
しかし、参照してはいけないところも参照できたり(下手をするとプログラムが落ちます=停止します)、プログラムを作ったヒトの意図を汲み取りづらくなったりするというしっぺ返しもあります。
通信も交通も生産もプログラムで制御する、社会インフラ自体がコンピュータシステムに強く依存する。そうした社会におけるプログラムの方向としては、手軽さよりも堅牢性を重視しなければならない。そうなると、型の定義、型計算を厳密にしてヘンテコなことが起きないようにプログラミング言語も進化してきたという流れです。
こうした言語、特に新しく登場してきている言語は数論、特に「圏論」とは無関係ではありません。ただ、真っ向から圏論に取り組むのはハードルが高いです、少なくとも私には。また、圏論が扱おうとしている範囲は非常に広いので、全てを俯瞰することは難しいと思います。圏論の持つ概念を掴めれば、プログラミングの基礎となる概念の理解に繋がります。また、きちんとしたプログラムを作るために必要な、型の定義を含む設計や、抽象化といったスキルの向上も望めると思います。
ネット上には良質な資料が沢山あります。そして我々は、それを簡単に手に入れることができるという便利な時代に居ます。もっと圏論に関して詳しく知りたいという素敵な動機が芽生えた方は、ぜひ下記の資料を参照してください。
・「圏論とプログラミング」by 稲見さん (5)
・「計算機科学のための圏論の基礎の基礎」 by Koga-san (6)
「他人任せ」「手抜き」と言われそうですが、筆者には、このお二方よりも上手く「圏論」を説明する自信がありませんので、ご容赦ください。
まとめ
前回(第4話)、今回(第5話)と2話を消費して「数学」「数論」的な話を書かせて頂きました。暗号も通信も数学で成り立っているのだよ、数学って身近なテーマで面白いよという辺りをお伝えできれば良いなと思っていますが、いかがでしたでしょうか?
「整数」「行列」「ベクトル」辺りは多少馴染みがあるとしても、「複素数」「テンソル」というと普通のヒトにとっては「?」が付きますよね? ましてや「群・環・体」「四元数」「圏論」なんて聞いたことがないかも知れません。しかし、これを機会に、そんな世界もあるのだ、とか、その単語どこかで聞いたことがあると思って頂ければ幸いです。
数学者であり、物理学者、天文学者でもある天才カール・フリードリヒ・ガウスさんの言葉で締めくくりたいと思います。
「数学は科学の女王であり、数論は数学の女王である」
「数論の法則は、目に見えて現れるものだが、その証明は、宇宙の闇に深く横たわっている」
(*1) 群論概念の知的必要性を生じさせる指導デザイン
https://www.edu.sugiyama-u.ac.jp/math/file-kaken/hamanaka3.pdf
(*2) 群論で解き明かすルービックキューブの数理
http://www.ivis.co.jp/text/20100901.pdf
(*3) 四元数の発見
ハミルトンさんはが奥さんと運河沿いの道を歩いている時に、四元数の概念が閃き、渡っていた石橋にi2=j2=k2=ijk=-1 という数式を刻んだそうです。これは事実で、現在もその橋には石碑が残っているそうです。逸話としては良い話なのですが、そんな夫を妻はどう思っていたのか? はあまり考えたくない私でした。
https://en.wikipedia.org/wiki/Broom_Bridge
(*4) 対象 と 射
「射」という日本語は良いとして「対象」は、筆者としてしっくりきません。
「象」あるいは「評」の方が私好みです。
まあ、私の好みで決めるべき話でもありませんので、どなたか、もっと良い言葉を適用して、定着させてください!
(*5) 「圏論とプログラミング」
https://qiita.com/inamiy/items/9af1da1faec22cd968f0
(*6) 「計算機科学のための圏論の基礎の基礎」
http://www.ivis.co.jp/text/20200325.pdf
白狐村塾話の過去の記事はこちら(合わせてお読みください)
CS白狐村塾(第1話)サイバーセキュリティに必須の技術、詳細に解説! その1
CS白狐村塾(第1話)サイバーセキュリティに必須の技術、詳細に解説! その2
CS白狐村塾(第2話)楕円曲線暗号について
CS白狐村塾(第3話)基礎から徹底解説! ストリーム暗号とは何か? RC4から、Salsa20、ChaCha20まで
CS白狐村塾(第4話)情報システムをリードするために、代数学の基礎を押さえよう!
サイバーセキュリティ白狐村塾は、新たなお話が公開されたときにメールマガジンにてご案内致します。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。

中村 健 (Ken Nakamura)
株式会社SYNCHRO 取締役 CTO
機械屋だったはずだが、いつの間にかソフト屋になっていた。
以前は計測制御、知識工学が専門分野で、日本版スペースシャトルの飛行実験に関わったり、アクアラインを掘ったりしていた。
VoIPに関わったことで通信も専門分野に加わり、最近はネットワークセキュリティに注力している。
https://www.udc-synchro.co.jp/
本文中に誤りがありましたので、下記の通り訂正いたしました。
誤:アルベール群 → 正:アーベル群
読者の皆様にご迷惑をお掛けしましたことを心よりお詫び申し上げます。






