ＣＳ四方山話（第23話）暗号を理解するための数学の世界その2
小学生からの数学シリーズ・第二弾

さて、今回も「小学校からの数学」シリーズ、その第２弾です。

前回の第１弾（ＣＳ四方山話 第22話）は如何でしたでしょうか？　本当に分かり易く書けたのだろうか？　等々、筆者は不安を払拭できないのですが、始めてしまったので続けます。お付き合い頂ければ幸いです。

復習（新解釈・小学１年生の前半）

前回は、自然数、加法（足し算・引き算）、単位元、逆元までを学びました。

　今回は、「群」をコンプ（コンプリート）するために、「結合則」と「閉じている」について学びましょう。

「群」とは

　集合Ｇとその上の二項演算 Ｇ・Ｇ＝Ｇ が「群」であるとは、以下の３つが成立することが条件です。

　①その二項演算に関して閉じている（任意のＧの元に対する二項演算の結果もＧの元である）
　②その二項演算に関して結合則が成り立つ
　③その二項演算に関して単位元が存在する
　④その二項演算に関して逆元が存在する

　小学１年生なので一般化せず、ここでは集合Ｇを整数とし、その二項演算を（狭義の）加法としましょう。

　③④は、第22話で確認しました。

　①に関して考察しましょう。

任意の整数２つを選んで足し算をしてみましょう。どんな整数２つを選んでも、その結果は必ず整数になりそうです。なる感じがします。きっとなるでしょう。

「きっと」ではいけないので証明する必要がありますが、まだ小学１年生なので証明は止めておきましょう。興味を持たれた方は「ペアノの公理」を調べてみてください(*1)。

②に関して考察しましょう。

結合則が成り立つというのは、下記のようなことです。

6+(3+1)=(6+3)+1

小学１年生のドリルにも同じ式が出てきます。感覚的には「当たり前」のことですね。
「当たり前」ではいけないので証明する必要がありますが、まだ小学１年生なので証明は止めておきましょう。興味を持たれた方は「ペアノの公理」を使って証明してみてください(*2)。

これで、整数に関しては、①②③④の性質を持つことが分かりました。
整数は「群 (group)」であるということになります。

もう１つ条件を増やしてみましょう。

⑤その二項演算に関して交換則が成り立つ

交換則が成り立つというのは、下記のようなことです。

6+3=3+6

①②③④⑤が全て成立する場合は「可換群」「アベール群 (abelian group)」と呼称します。

ちなみに、
①②だけ成立する場合は「半群 (semigroup)」、
①②③だけ成立する場合は「モノイド (monoid)」と呼称します。

少し脱線しました。こうした名称は、小学１年生では覚えなくて良いですね。ただの暗記ですから。　小学１年生では、下記を知ってもらえば充分でしょう。

「数」というものには「仲間」があること。
整数の加法は「群」で閉じていること。
いろいろ足す場合、どこから足しても同じであること。→ 結合則
足しても変わらない「数」があること。→ 「0」の存在
「足す」の逆の操作＝「引く」があること。→ 「逆元」の存在

まとめ

「新解釈・小学１年生」と言えるだけに「分かり易く」書けたでしょうか？

今回で、「群」までを学んだことになります。「それがなんなの？」「群が分かってなにか意味があるの？」というご意見もあろうかと思います。もちろん、社会の全員が数学に通じている必要はありません。ただ、IT、ICT（ネットワークやコンピュータ）に関わる皆さんには、なんとなくでも、単語を聞いたことがあるだけでも充分なので知っていてくださると良いなと思っています。また、これから、未来を切り拓く方々には、さらに学んで頂けると嬉しいなと思っています。

数学、数の世界は、自然、整数から、実数、複素数へと広がっていきます。群も、環、体、圏と広がります。そうした広がりを楽しんで頂けると有り難いです。

さて、また「前回の予告」を外してしまいました。繰り上がり・繰り下がりの話は次回に譲ります。従来からの読者の方は「ああ、いつものこと」だとご寛恕くださることを期待しています。

四方山話

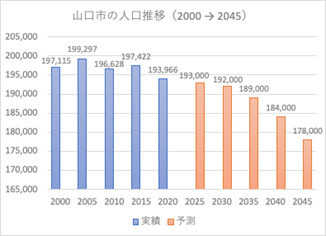
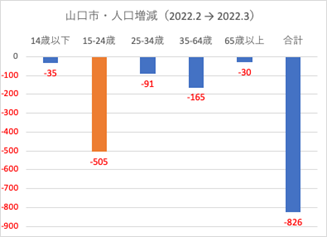
前回（第22話）の四方山話で島根県益田市さんの話題に触れました。「環境を維持するためには、地元の経済的な活性を維持向上することが必要です」とコメントしました。そのためには、働く環境を作って、働くヒトが活動することが求められます。 　島根県益田市さんを含め、地方都市はどこも同じ課題を抱えています。私が月の2/3を過ごす山口市も同じです。人口総数は減少傾向にあり、若い世代の流出が多いことには留意しなければなりません。豊かな住環境に加えて、将来に夢を持てる労働環境を作り、「地方の真に豊かな環境で暮らし、世界トップレベルの報酬を得ること」を実現できればと思っています。

---

（*1）ペアノの公理

一般的なペアノの公理とは「Ｎに対して、Ｎ＋１が存在する」と定義することです。
これは「公理」なので、証明は不要です（そういう世界を作ったということになります）。
このペアノの公理と、数学的帰納法を用いて、整数が加法に関して閉じていることを証明可能です。

（*2）結合則の証明

数学的帰納法を用いて　Ｘ＋（Ｙ＋Z）＝（Ｘ＋Ｙ）＋Ｚ が成立することを証明します。

Ｚ＝１とすると、Ｘ＋（Y＋１）＝（X＋Y）＋１　となります。

Z＝Ｋのとき成立するならば、Z＝Ｋ＋１のときにも成立することを示せば良いです。
Z＝Ｋのとき結合法則が成立すると仮定すると、
　Ｘ＋（Ｙ＋（Ｋ＋１））
　＝Ｘ＋（（Ｙ＋Ｋ）＋１） ・・・加法の定義式より
　＝（Ｘ＋（Ｙ＋Ｋ））＋１ ・・・Z＝１の場合は証明済
　＝（（Ｘ＋Ｙ）＋Ｋ）＋１ ・・・帰納法の仮定より
　＝（Ｘ＋Ｙ）＋（Ｋ＋１） ・・・加法の定義式より
　となり、Ｋ＋１のときにも成立します。

---

ＣＳ四方山話の過去の記事はこちら（合わせてお読みください）

---

サイバーセキュリティ四方山話の最新話は、メールマガジンにてもご案内致しています。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。