CS四方山話(第26話)暗号を理解するための数学の世界その5
前回の第4弾(CS四方山話 第25話)で、(新基準)小学1年生の課程を修了しました。今回からは「小学校からの数学」シリーズ・第5弾として、(新基準)小学2年生の課程に進みます。
小学2年生と言えば「九九」ですね。筆者の時代も「九九」は小学2年生で登場しました。それを思い起こすと、小学2年生の時の教室の情景が浮かんできました(記憶って不思議なモノです)。学校の中では南東角で2階の明るい教室でした。ということで、まずは「九九」からです。
九九
「九九」は、ご存知の通り1桁の掛け算です。もう少し厳密に言えば、10進数1桁の自然数の積です。小学1年生の課程では、加法(足し算、引き算)のみを扱っていたのですが、ここで乗法(掛け算)が登場します。「群」の世界から「環」の世界に踏み出したことになります。
「九九」の学習とは、ご存知の通り、下記のような表を覚えるということになります。
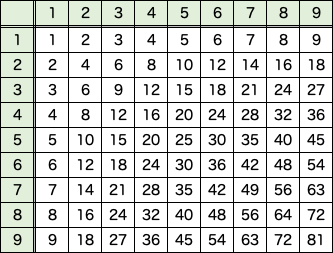
「にんいちがに」「ににんがし」「にさんがろく」…「さんにがろく」…「くくはちじゅういち」
論理的な背景は考えずに、語感で覚えるという方法論。つまりは、丸暗記ということですね。数も81と限定されていますし、暗記も現実解としては悪くないと思います。
暗記する量を節約するために、少し数学的なアプローチを考えてみましょう。
この表を眺めてみると、対角線(赤い部分)に対して線対称であることが分かります。
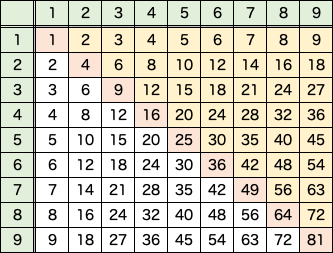
これは、この二項演算に関して「交換則」が成り立つということです。
n × m = m × n ということで、暗記する量は、81 から 45 まで減ります。
もう1つ、1の段(青い部分)は、掛けた数字と同じ値になります。
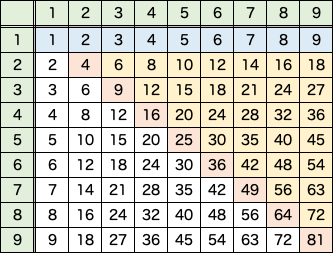
乗算において「1」は単位元です。「1」を掛けても数は変わりません。これさえ覚えておけば、1の段は暗記しなくても良くなります。これで、暗記する量は、45 から 36 まで減ります。81 → 36 と暗記量は 約55% 削減、半分以下になりました。
暗記量の圧縮はここまでですが、この表には「もう1つ気が付くべき点」があります。
表の中に、元の数 {1〜9} と同じモノが登場します。式にすると下記の通りです。
4 = 2 × 2
6 = 2 × 3 = 3 × 2
8 = 2 × 4 = 4 × 2
9 = 3 × 3
4, 6, 8, 9 は、他の数の乗算(掛け算)の結果であるということです。つまり、素数ではないということになります(素数とは、正の約数が1とその数自身である数で、かつ1でない自然数です)。
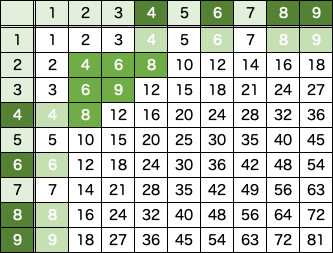
約数、倍数、素数
現在の教育課程では、約数、倍数、素数、最大公約数、最小公倍数などは小学5年生で登場します。それも考慮に入れて、(新基準)小学2年生では、これらを詳しく掘り下げることは止めておきます。しかし、「九九」の表からこうした内容を読み取ることが可能ということには、(新基準)小学2年生でも触れておきたいと思います。
「2の段」の数は、すべて「2の倍数」(2の仲間)ですし、「3の段」の数は、すべて「3の倍数」(3の仲間)です。そして、「2の段」には「4」「6」「8」が含まれるので、「4の段」「6の段」「8の段」の数は、すべて「2の倍数」(2の仲間)ということになります。
虫食い算、素因数分解
2年生の課程には「虫食い算」というものが登場します。これを「九九」応用すると次のような問題になります(□に入る数を答えるという問題です)。
3 × □ = 6
□ × 7 = 35
5 × □ = 40
「九九」をしっかり覚え込む方法論として有効でしょう。
しかし、この問題には、暗号理論に繋がる重要な概念が含まれています。
上記の問題を下記のように置き換えてみます。
① □ × □ = 6
② □ × □ = 35
③ □ × □ = 40
この問題の答えも「九九」の表から求めることができます。
①の答えは、2 × 3 = 6 、3 × 2 = 6
②の答えは、5 × 7 = 35 、7 × 5 = 35
③の答えは、5 × 8 = 40 、8 × 5 = 40
もう少し踏み込んで見ましょう。
「8」は「九九」の表の中にあります。
2 × 4 = 8、4 × 2 = 8
そして、「4」も「九九」の表の中にあります。
2 × 2 = 4
これを整理すると下記のようになります(交換則によって、同一になる組み合わせは省略します)。
40 = 5 × 8
40 = 5 × ( 2 × 4 )
40 = 5 × ( 2 × ( 2 × 2 )
40 = 5 × 2 × 2 × 2
40 = 5 × 23
□ だけの掛け算(乗算)で表現され、その□の中を求めることは「素因数分解」と呼ばれます。
素因数分解は、中学3年生の課程で学ぶことになっているので、ここでは詳説しません。しかし、81マスという小さな「九九」の表の中にも、素因数分解に繋がる要素があるということは知って頂けると嬉しいですし、面白い! と思って頂ければ、さらに嬉しいです。
まとめ
今回(第26話)は「九九」とその周辺の話でした。「小学2年生の数学」には、「九九」以外にも数学的に学ぶべき要素がありますので、次回(第27話)はそれらを扱おうと思います。
四方山話
本文で「素因数分解が暗号理論に繋がる」と書きましたので、四方山話では、その点に触れたいと思います。
「九九」のレベルでは、素因数分解は簡単でした。
—————————————-
713 = 23 × 31
1591 = 37 × 43
32111 = 163 x 197
—————————————-
この辺りまでも簡単です。
暗算では無理かも知れませんが、簡単なプログラムでごく短時間で解けます。
しかし、次の数(10進数)ではどうでしょうか?
95864541996095827002792437249683058156299989840410833802698015890151999531801
この数を素因数分解すると、2つの素数になります(ご自慢のコンピュータで解いてみてください。答えは次回でw)。
もちろん解くことは可能です。しかし、現在のデジタルコンピュータの中でも高速なモノを使っても短時間でその解を得ることはできません。「解けるけど、簡単には解けない」という性質を活かした仕組みが、現在の世界のあらゆるところで使われている「RSA暗号」「楕円曲線暗号」なのです。 この辺りをもっと詳しく知りたいという方は「CS白狐村塾(第1話-その2)」をお読みください。
CS四方山話の過去の記事はこちら(合わせてお読みください)

中村 健 (Ken Nakamura)
株式会社SYNCHRO 取締役 CTO
機械屋だったはずだが、いつの間にかソフト屋になっていた。
以前は計測制御、知識工学が専門分野で、日本版スペースシャトルの飛行実験に関わったり、アクアラインを掘ったりしていた。
VoIPに関わったことで通信も専門分野に加わり、最近はネットワークセキュリティに注力している。
https://www.udc-synchro.co.jp/
サイバーセキュリティ四方山話の最新話は、メールマガジンにてもご案内致しています。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。






