CS四方山話(第27話) 暗号を理解するための数学の世界その6
小学校からの数学シリーズ・第6弾
「小学校からの数学」シリーズ・第6弾です。前回の第5弾(CS四方山話 第26話)で (新基準)小学2年生に進級し、「九九」を学びました。四方山話に記載した内容ですが、九九が素因数分解に繋がり、更に暗号理論に繋がることも知りました。小学2年生では「九九」以外のことも学びます。今回は、その辺りを見ていきましょう。
時刻と時間
大人でも、時刻と時間を、表現として明確に区分しない人もいます。しかし、この2つは別モノです。このことは、現行の小学2年生の課程でも教わります。
「9時ちょうど」「9 時15分」「9時半」が示すモノは「時刻」です。一方、カップラーメンにお湯を注いで待つ「3分」、「9時から9時半までの30分」が示すモノが「時間」です。
もう少し深掘りしてみましょう。
時刻と時刻の間の「所要時間」が「時間」です。たとえば、同じ「2」でも「2時」と「2時間」の2種類が存在するという理解がまずは必要です。
「時刻」は state(状態)を表しており、「時間」は action(操作)を表しています。state と action は全くの別モノです。その概念を表す材料として、時刻と時間という例は教育上で有用だと思います。
「2時から2時間経ったら何時でしょう?」という問題を式で表現すると「2+2=4」と書きたくなるかも知れません。しかし、前述の通り「2時」と「2時間」は別モノ、つまり、次元(dimension)が異なるので、足し算(2項演算)はできません。
どうしても足し算に持ち込みたいとすると、以下のような表現になるでしょう。
2時 (state), 2時間 (action)
= ( 0時 (state), 2時間 (action) ), 2時間 (action)
= 0時 (state), ( 2時間 (action), 2時間 (action) )
= 0時 (state), ( ( 2 + 2 ) 時間 (action))
= 0時 (state), 4時間 (action)
= 4時 (state)
圏論との関係
state を object(対象)、action を allow(射)と置き換えると、これは正に「圏論(category theory)」の世界です。
圏(category)は1900年代半ばに登場した概念です。圏論は2000年以降、数学、コンピュータサイエンス、哲学などの広い分野で着目されている概念です。これは筆者の推定ですが、圏論では図(diagram)による視覚的な表現を行います。この表現によって数学全般を分かり易く表せるという辺りがウケているのではないでしょうか。
「圏論は数学を鳥の視点で観察できる。上空からは細部は見えないが、地上からでは把握できないパターンを(鳥の目では)捕らえられる」「集合論の内的視点に対し、圏論はその対象を他の対象とどのように関係するかによって特徴づける外的視点をとる。いわば,圏論は集合論の『もの』への視点から『こと』への視点への移行と言えるであろう」というようにも表現されています。
時刻の表現には action を利用したものもあります。
たとえば「10時10分前」という表現です(英語では ” 10 to 10 ” と表現します)。
言うまでもなく 9時50分 という state です。
「9時50分」は「9時 (state), 50分経過 (action)」を表していますが、「10時10分前」は「10時 (state) 10分手前 (action)」を表しています。指し示す state は同じですが、その経路は異なるということになります。
圏論では、この2つの経路の違いを扱います。 小学2年生の段階でこうした概念を理解することは少し難しいかも知れませんが、時刻と時間という題材で、圏論への端緒を作っておくことには意味があるでしょう。大人の皆さんは、時には「鳥の視点」を意識してみることも何かの役に立つでしょう(多分……。ちょびりは)。
数学の世界
時刻と時間の話もそうですが、我々は「暗黙の了解」といったもので、なんとなく見過ごしていることがいろいろあります。それらをキチンと定義してみようというのが数学の世界です。
「何を面倒なことを……」「世の中は理屈ではなく情念なんだ」というご意見もあろうかと思います。しかし、DXが叫ばれ、情報インフラなしには成立しない社会に突き進んでいく世の中では、数学を視野外に押し出すことは難しくなりつつあります。鷹揚さも情熱も必要ですし、全員が数学者になる必要はありませんが、数学的なものの見方の必要性は高くなっていると思います。
たとえば「林檎が3つ、蜜柑が2つあります。全部でいくつでしょう?」という問題にはツッコミを入れる必要があります。なぜ、林檎と蜜柑の個数を足し算できるのか?ここに違和感を持つことが必要ですし、きっとそう思う小学生もいることでしょう。
問題が下記のような形であれば、違和感は消えるのではないでしょうか?
林檎と蜜柑は、果物の一種です。
さてここに、林檎が3つ、蜜柑が2つあります。
ここには、果物はいくつあるでしょう?
林檎と蜜柑が「果物の一種」であるという暗黙の了解を明示的に定義したということになります。
では「ジャガイモ3つと、豚さん2頭とを一緒にするとどうなるでしょう?」
この回答として「5つのオブジェクトが存在します」という答えもあるでしょうし、「ジャガイモは豚さんに食べられて、豚さん2頭になります」という答えもあるでしょう。答え、つまり解が一意に定まらないのは、きちんとした定義がないからです。こうした曖昧さを排除して行くのが数学の世界です。
まとめ
今回(第27話)は、小学2年生の課程で登場する時刻・時間の話から、圏論の触りの辺りに踏み込んでみました。主軸とは異なる四方山話(前回の宿題? の答え合わせ)で文字数を消費するという(ありがちな?)パターンになっておりますがご容赦ください(サボっている訳ではありません)。
小学2年生の課程には、まだ取り上げるべき内容がありますので、次回(第28話)も引き続き小学2年生です。
四方山話
前回の宿題? の答え合わせをしましょう。
問題は「次の数(10進数)を素因数分解してください」でした。
95864541996095827002792437249683058156299989840410833802698015890151999531801
皆さんは、答えに辿り着いたでしょうか?
正解は、下記です。
| 324624077823850574837710456151279624363 295309401073183512428347116869816798027 |
この正解は本当?(= 本当に素数?)というご意見もあろうかと思います。素数かどうかを確認する方法としては「フェルマー・テスト」「ミラーラビン・テスト」という方法があります。
フェルマー・テスト:
p を素数とするとき、p と互いに素な整数 aに対して以下が成り立つ
αp-1≡1(mod p)
ミラーラビン・テスト:
p を素数とするとき、
p-1=2s・dと表せる(sは正整数、d は奇数)。
このとき、1 ≦ a ≦ ー1 を満たす a に対して以下が成り立つ
2d≡1 ( mod p )
または、ある 0 ≦ r ≦ s ー 1 に対して以下が成り立つ
α2r-d≡-1 ( mod p )
いずれの方法も、試行によって素数か否かの判定を行う方法です(限られた試行回数では、100%の判定はできないということになります)。
実際に素数かどうか知りたい場合は「巨大数向け素数判定機」を試してみてください。
https://tools.m-bsys.com/calculators/primality_test_for_large_number.php
各テストのロジックを知りたい場合は「フェルマー・テスト」「ミラーラビン素数判定法」などが参考になるでしょう。
https://qiita.com/srtk86/items/609737d50c9ef5f5dc59
テストとは方向性が異なりますが、N 以下の素数を見つける方法としては「エラトステネスの篩 (ふるい)」が有名です。分かり易い方法論なので、少し説明しましょう。
手順は単純です。
① 2 から n までの整数のリストを作る
② 生き残っている数の中で一番小さい(かつまだ p として使われていない)ものを新たに p とする(最初は 2 です)
③ p 以外の p の倍数をリストから取り除く
④ 「②③」の操作を繰り返し、p が √n よりも大きくなったら停止。その時点でリストに残ったものが整数。
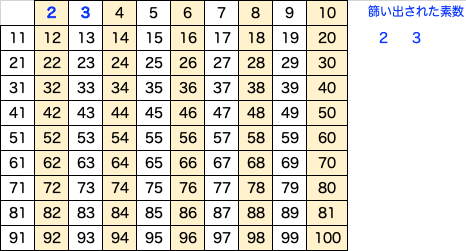
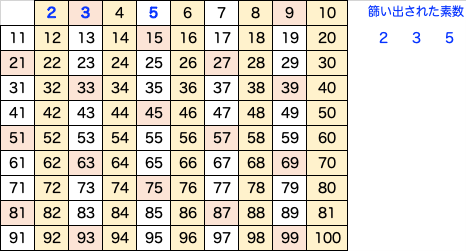
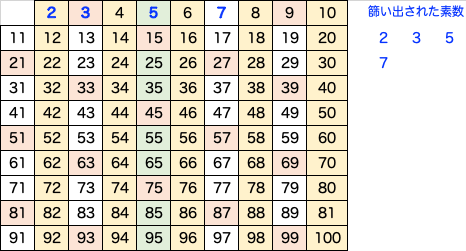
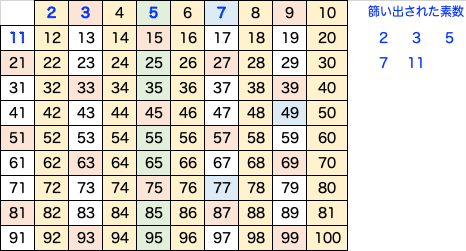
:(この繰り返しです)
CS四方山話の過去の記事はこちら(合わせてお読みください)

中村 健 (Ken Nakamura)
株式会社SYNCHRO 取締役 CTO
機械屋だったはずだが、いつの間にかソフト屋になっていた。
以前は計測制御、知識工学が専門分野で、日本版スペースシャトルの飛行実験に関わったり、アクアラインを掘ったりしていた。
VoIPに関わったことで通信も専門分野に加わり、最近はネットワークセキュリティに注力している。
https://www.udc-synchro.co.jp/
サイバーセキュリティ四方山話の最新話は、メールマガジンにてもご案内致しています。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。






