暗号を理解するための数学の世界 CS四方山話（第40話）

「小学校からの数学」シリーズ・第19弾です。今回は、小学６年生の３回目になります。前回予告の通り、テーマは数学定数の筆頭「円周率（π）」と「変数」です。

7～9月と仕事でのイベントが多く（←言い訳）、前回執筆から４ヵ月も空いてしまいました。10月28日 から
「 JAPANSecuritySummit 2025 」(JSS2025) が始まるということもあり、慌てて書き始めております。今年もJSS2025 にて「ＣＳ四方山話 Live Session」を開催させて頂きますので、こちらよろしくお願い致します、という意味が込められています。

https://jss2025-yomoyama.peatix.com

円周率とは？

さて円周率とは何でしょう？
　　　円周率 = 円周 ÷ 直径 です。
図で表すと次のようになります。

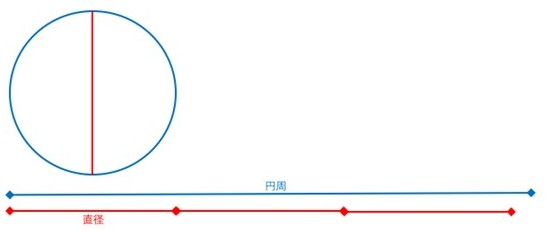
概念としては非常に簡単です。故に小学校でも円周率が登場するのです。

小学校における円周率

円周を求めるという場面（問題）は少ないですが、円の面積を求めるという場面は多くあるでしょう。円の面積を求めるためには、円周率が必要になります。

小学校では「円の面積を求めましょう」という問題が出されます。

では、円の面積はどのように求めるのでしょう？

円を細かく切り分けて並べ替えます。より細かく切り分けると、並べ替えた図形は長方形に近づきます。無限に細かく切り分けて並び替えたとすると長方形になります。

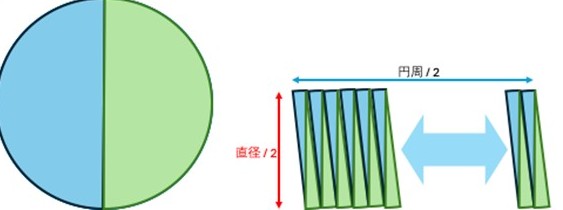
この時の長方形の辺の長さは、円の半径 と 円周の 1/2 になります。

　　　円の面積
　　　　= 円の半径 × 円周 × 1/2
　　　　= 円の半径 × （ 円の直径 × 円周率 × 1/2 ）
　　　　= 円の半径 × （ 円の直径 × 1/2 ）× 円周率
　　　　= 円の半径 × 円の半径 ×円周率

　小学校では、この式を使って、円の面積を計算します。

　現在の日本の教育課程では、円周率 = 3.14 として計算しましょうということになっています。

　従って、直径20cm の 円の面積は 10 × 10 × 3.14 = 314 平方センチメートル となります。

円周率と「π」

　小学校では「円周率 = 3.14」を定義していますが、これはあくまでも「近似」です。

だいたい 3.14 ぐらいということで、真の値はではありません。では、真の値はいくつなのでしょうか？　これは小数では記述できませんし、分数でも記述できません。そう、円周率は「無理数」なのです。

この無理数を、いつも「円周率」として記述するのは数式的には美しくありません。数式上、円周率は「π」と表現することになっています。

では何故、円周率を「π」で表すのか？

ギリシャ語で直径を意味する「περｉμετρος（ペリメトロス）」の頭文字をとったもので、18世紀の数学者William Jones（ウィリアム・ジョーンズ）が始めて使ったそうです（彼は、πを始めて使ったことで歴史に名を残しました）。その後、大御所 Leonhard Euler（レオンハルト・オイラー）もこのπを使うようになったことで普及することになりました。

円周率はどのように求めるのか <1>

前述の通り、円周率πは無理数です。では、このπはどのようにして求めるのでしょうか？

古代バビロニアでは、天体の位置などを計算するために既に円周率を使っていたそうです。この頃は、円周率はおおよそ「３」として計算していたようです。

その後、古代ギリシャの数学者アルキメデスは、円に内接する正多角形、円に外接する正多角形を使って円周率を求める方法を使い、円周率はおおよそ「3.14」としたそうです。このときに用いた正多角形は「正96角形」だったそうです。

正96角形を図にするのは面倒なので、ここでは正６角形と、正12角形を例にとります。

まずは、正６角形。

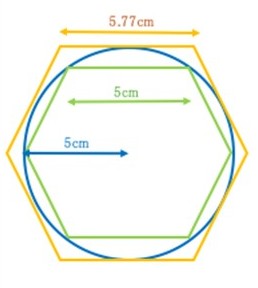
直径10cmの円に内接する正６角形の１辺の長さは5cmで全周は30cmになります。一方、直径10cmの円に外接する正６角形の１辺の長さは約5.77cmで全周は約34.64cmになります。従って、3 < 円周率 < 3.464 ということになります。

次にもう少し精度を上げるために、正12角形を使います。

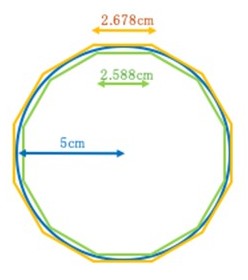
直径10cmの円に内接する正12角形の１辺の長さは約2.588cmで全周は31.056cmになります。また直径10cmの円に外接する正12角形の１辺の長さは約2.678cmで全周は約32.136cmになります。

従って、3.1056 < 円周率 < 3.2136 ということになります。

この方法で正多角形の辺の数を増やし、アルキメデスは「3.14よりも少し大きい」と特定したようです。

日本では、江戸時代の数学者の関孝和が正131,072角形を使って「3.14159265359よりも少し小さい」と計算したそうです。江戸時代ですから当然手計算です。根気の要る作業ですね（筆者には無理です）。

円周率はどのように求めるのか <2>

コンピュータが登場すると円周率の桁数は飛躍的に伸びます。

　　2019年: 米グーグルが31.4兆桁。
　　2021年: スイスの研究チームが62.8兆桁。
　　2024年9月: スイスの研究チームが100兆桁。

そして、2025年6月にはカナダのライナスメディアグループが300兆桁の円周率を計算しました。

ちなみに、このプロジェクトを支えたのは、日本の半導体メーカーのキオクシアで、記録達成のための記憶媒体として大量のSSDを提供したそうです。キオクシアのSSDを含め演算システムは8ヵ月弱の間、無停止で安定稼働したそうです。

コンピュータを用いて円周率を計算する方法は、大別して２つあります。

１つは「モンテカルロ法」、もう１つは「公式による方法」です。

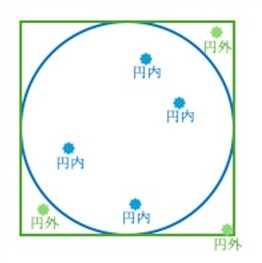
モンテカルロ法は単純です。正方形とその正方形に内接する円を描きます。この正方形内にランダムに点を打ち、その点が円内にあるのかの判定を行います。正方形と円の面積比は １：π/4 となるので、円内に点が入った確率を４倍すれば、それが円周率ということになります。

円周率πには美しい性質があります。πに関連した無限級数を２つ挙げておきます。

１つ目は「マーダヴァ・グレゴリー・ライプニッツ級数」（マクローリン展開の１つ）です。

π 4 ＝ 1 1 − 1 3 ＋ 1 5 − 1 7 ＋ 1 9 − ⋯

２つ目は「オイラー級数（バーゼル問題）」です。

π² 6 ＝ 1 1² ＋ 1 2² ＋ 1 3² ＋ 1 4² ＋ 1 5² ＋ ⋯

どちらも、とても美しいですね。

美しさからは少し遠ざかりますが、チュドノフスキーの公式による計算が2000年頃から主流でした（チュドノフスキーの公式は, ラマヌジャン型の級数です）。

\[ \frac{1}{\pi} = \frac{12}{\sqrt{640320^3}} \sum_{n=0}^{\infty} \frac{(-1)^n (6n)! (13591409 + 54514012n)} {(3n)! (n!)^3 \times 640320^{{3n}}} \]

級数を使った計算は、目標桁数を N とすると  という計算量を必要とします。Nが100万辺りまで来ると苦しくなります。

代わって着目されたのが「算術幾何平均 (AGM = Arithmetic−Geometric Mean)」を用いた方法です。AGMでは計算量は 程度となり、2000年までに１兆桁まで伸びました。

その後「Binary Splitting」という手法が登場します。従来は級数の各項を多倍長の小数で表現して計算していましたが、「Binary Splitting」では分数のまま計算を進めて行きます。この方法で、級数を用いた場合でも計算量は程度に落ち着きました。現在は「チュドノフスキーの公式」＋「Binary Splitting」が円周率計算の主流のようです。

変数

完全に「小学校」の範囲を逸脱した話が続きましたので、路線を「小学６年生」に戻します。小学校最後の話題は「変数」です。

リンゴ１個は150円です。リンゴを□個買った時、合計いくらになるでしょう？

　　　150 × □ = 合計値

　合計値は 600円 でした。

　　　150 × □ = 600

　リンゴをいくつ買ったでしょう。

　　　□ = 4

つまり、4個と答えるでしょう。この時の □ が変数です。

　数式的に書くと 150ｘ = 600 となり、ｘ = 600 / 150 = 4 と解けます。

　表現が □ か ｘ かの違いだけで、どちらも変数です。

中学校以降では「算数」ではなく「数学」となり、「方程式」や「関数」が登場します。これらは「変数」がないと表現しにくくなります。「変数」という概念は理解しておく必要があります。

また、物事を抽象化して考えることも数学では必要です。リンゴの個数としての数ではなく、具体的な次元を持たず、どんな数字でも扱えるモノと考える。それが変数です。

プログラミングを行うためには「変数」が必須です。中学校では、Scratch、Pythonなどのプログラミング言語にも触れることになると思います。このときにも変数が必要になります。

前回（第39話）で「小学校 → 中学数学への接続の仕方」ということに言及しましたが、「変数」に触れておくことも、この接続の「橋渡し役」ということになるでしょう。

まとめ

今回は、小学６年生の課程で登場する「円周率」「変数」に関して取り上げました。「小学校からの数学」シリーズは「第19弾」とキリが悪いですが、「ＣＳ四方山話」としては「第40話」でキリが良いです。ということで、「小学校からの数学」シリーズは今回で終了とさせて頂きます。

「小学校からの数学」シリーズは 2023年3月からで、2年半程続けさせて頂きました。ご愛読頂いたみなさま、本当にありがとうございました。

２年半、ＣＳ（サイバーセキュリティ）と離れてしまっていましたので、次回（第41話）は一旦ＣＳの話に立ち戻りたいと思います。しかし「小学校」をやってきましたので、いずれ「中学校」もやって行きたいと思います。引き続き、よろしくお願い致します。

また「ＣＳ四方山話」の電子書籍 第１段「サイバーセキュリティ四方山話 VOL.1」は、2024年10月1日に ConTenDo さんから発売になっております。こちらも、よろしくお願い致します。

https://contendo.jp/store/contendo/Product/Detail/Code/J0010582BK0159582001

第２段も鋭意執筆中です！　が、相変わらず進行中というステータスです (^^;;

雑談

私が勤務するCSCC（サイバーセキュリティ対策センタ）では、春と秋にBBQを行っています。一般社員だけでなく、社員のご家族やご友人も参加可能というスタイルです。今回は、山口の友人が所有している俵山のスペースを利用させて頂きました。

---

サイバーセキュリティ四方山話の過去の記事はこちら（合わせてお読みください）

サイバーセキュリティ四方山話の最新話は、メールマガジンにてもご案内致しています。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。