暗号を理解するための数学の世界 CS四方山話(第39話)
「小学校からの数学」シリーズ・第18弾です。今回は、小学6年生の2回目になります。前回予告の通り、テーマは「並べ方と組合せ方」になります。
「並べ方と組合せ方」vs「順列組合せ」
小学6年生の「並べ方と組合せ方」と中学以降の「順列組合せ」を比較してみました。なぜならば、筆者にとっては「並べ方と組合せ方」という括りに馴染みがなかったからです。
扱うテーマは同じです。
「並べ方」は、並べる順番に意味がある場合で、これは「順列」(Permutation)です。
「組合せ方」は、順番は対象としない組合せで、これは「組合せ」(Combination)です。
では、どこが違うのでしょう?
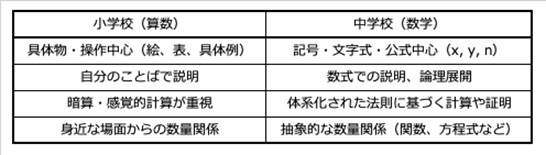
1つは「表現方法」です。小学6年生では、図に表したり、表に整理して理解を進めます。これに対して、中学以降の数学では、数式や記号で表現したり解いたりします。 もう1つは「内容の深さ」です。小学6年生では、比較的小さい集合を例にします。また、具体例のみを扱います。これに対して中学以降の数学では、抽象化された大きな数や汎用的な公式を扱います。
並べ方を表や図にしてみる
3人の生徒がいます。この3人が順番に走る場合、その順番はいくつあるでしょう? 表にすると、こんな感じですね。
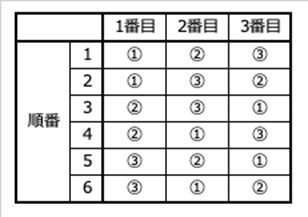
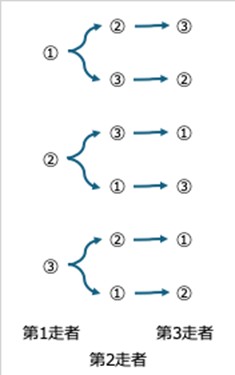
図にすると、こんな感じでしょうか。「櫛形図」というそうです(筆者はこの呼称は知りませんでした。どこかで教わったかも知れませんが)。
4つの数字 { 1, 3, 5, 7 } から2桁の数字を作るという問題を考えてみます。表にすると、こんな感じですね。
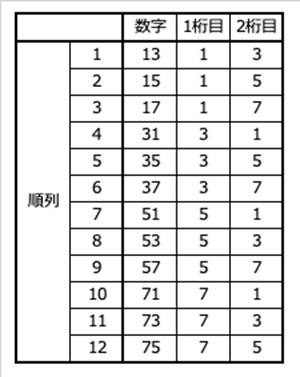
組合せを表や図にしてみる
4チームがあります。リーグ戦を行うとすると、試合数はいくつになるでしょう。組合せは「表」のほうが分かりやすいでしょう。
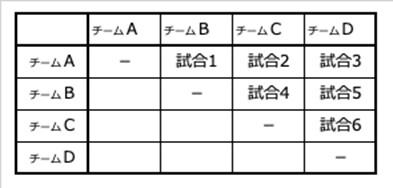
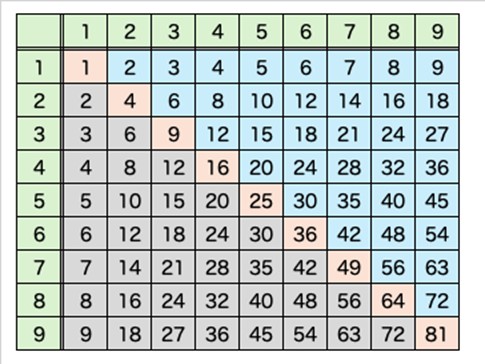
このパターンは九九も同じですね。整数の乗法は可換なので、九九で登場するパターンは「36」になります。組合せとしては、図の青色の部分になります。
数式を使って一般化(小学校→中学校)してみる
3要素の順列であれば、小学校の流儀に沿って書き出してみるのが分かりやいですね。小学校の範囲からはみ出ますが、3人が 10人 になっただけでも話は変わって来ます。
10人生徒がいます。この10人が順番に走る場合、その順番はいくつあるでしょう? この答えは 3,628,800 です。この場合には表や図で書き出そうとすると日が暮れます。いや、徹夜しても終わらないかも知れません。
3人が 100人 になったとすると……。その組合せの数は、9.33 × 10157というとてつもない数になります。順列(Permutation)を一般化する、つまり数式で表すと mPn となります。
値としては、m! (m − n)!
となります。3要素の順列は
3P3 = 3! 0! = 3! 1 = 3 × 2 × 1 = 6
です(ちなみに、0! の階乗 は 1 です。これは、数学上の 決まり事 です (※1))。10要素の順列は
= 3,628,800です。100要素の順列は
≒ 9.33
です。
続いて組合せの一般化についても考えてみましょう。クラスに 40人 の生徒がいます。この40人の中から、クラスの代表5名を選出するとして、その組合せはいくつあるでしょう?
答えは 658,008 です。先ほどの問題よりは小規模ですが、これも徹夜しても終わらないかも知れません。 組合せ(Combination)を一般化する、つまり数式で表すと mCnとなります。値としては、
m! n! × (m − n)!
となります
クラス代表の問題は、下記となります。
40! 5! × 35! = 40! 35! ÷ 5!
= 40 × 39 × 38 × 37 × 36 5 × 4 × 3 × 2 × 1 = 658,008
小学校→中学数学への接続の仕方
ChatGPT 4o が、偉そうに「必要であれば、小学校→中学数学への接続の仕方もご紹介できます。ご希望ありますか?」とか言ってくるので、話を聞いてみることにしました。
「小学校 → 中学数学への接続の仕方」は、小学校で学んだ算数的な“具体・操作的”な考え方を、中学校の“抽象・記号的”な数学にどう橋渡しするかという非常に重要な教育上のテーマです。特に中学1年生の数学につまずく多くの生徒は、この“接続のギャップ”がハードルになることが多いため、意図的な接続設計が必要とされています。
ふむふむ、なるほど..。
まとめ
今回は、小学6年生の課程で登場する「並べ方と組合せ方」をテーマに、「分数」の掛け算と割り算に関して取り上げました。さて次回(第40話)は「円の面積」と「文字と式」に関して学びます。数学定数の筆頭「円周率(π)」が登場します。また変数も登場します。引き続き、ご購読を頂ければ幸いです。
また、「CS四方山話」の電子書籍 第1段「サイバーセキュリティ四方山話 VOL.1」は、2024年10月1日に ConTenDo さんから発売になっております。こちらも、よろしくお願い致します。

https://contendo.jp/store/contendo/Product/Detail/Code/J0010582BK0159582001
第2段も鋭意執筆中です! まだ進行中です (^^;; 遅筆でスミマセン..。
補足
(※1) 0 の階乗(0!)= 1
直感的には「0 じゃないの?」「何故 1?」と思います。直感には合いません。
平たく言うと、これは「定義」つまり「きめごと」なのです。
数学的な「整合性」を守るための「定義」なのです。
階乗の再帰的な定義としては となります。これは、直感に合いますね。
1! = 1 これは OK です。
これに再帰的な定義を当てはめると、下記となります。
1 = 1!
両辺を 1 で除算すると、
1 = 0!
ということになります。
雑談
この「雑談」を執筆しているのは6月中旬です。
前回(第38話)の雑談でご紹介した湯田温泉こんこんパーク」(https://www.konkon-park.com/)が6月1日にオープンしました。筆者の(山口の)自宅から至近ですので、休日にはこんこんパークのテラスで遊ぶ子供達の声が聞こえてきて良い感じです。






さて、来たる8月28日には、筆者が所属する山口の「サイバーセキュリティ対策センター(CSCC)」としてのイベントを開催します。この場をお借りして、ご案内させて頂きます。
フォーティネットジャパン合同会社と弊社とのビジネスアライアンス発表会を山口県山口市にて開催する運びとなりました。
日時 : 8月28日(木)15時~
会場 : 山口県山口市 ニューメディアプラザ山口 多目的シアター
イベントの構成としては、
第一部 15時00分~ 山口県のイベント (知事も登壇)
第二部 16時00分~ SYNCHRO & FORTINETのイベント
第三部 17時30分~ 懇親会 (知事も参加)
という3部構成になっています。
是非、現地でご参加ください。とはいえ遠方ですので、online配信も準備致しました。現地までお運び頂くことが難しい場合は、online(15:00 – 17:30)のみでもご参加頂ければ幸いです。
添付のflyer にも記載がありますが、申し込み page は下記となります。https://forms.office.com/r/rGrnjT1PM6

サイバーセキュリティ四方山話の過去の記事はこちら(合わせてお読みください)

中村 健 (Ken Nakamura)
株式会社SYNCHRO 取締役 CTO
機械屋だったはずだが、いつの間にかソフト屋になっていた。
以前は計測制御、知識工学が専門分野で、日本版スペースシャトルの飛行実験に関わったり、アクアラインを掘ったりしていた。
VoIPに関わったことで通信も専門分野に加わり、最近はネットワークセキュリティに注力している。
https://www.udc-synchro.co.jp/
サイバーセキュリティ四方山話の最新話は、メールマガジンにてもご案内致しています。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。






