暗号を理解するための数学の世界その8 CS四方山話(第29話)
小学校からの数学シリーズ・第8弾
「小学校からの数学」シリーズ・第8弾です。今回から「小学3年生」に進級しました。7話(7回)を使って、小学校の課程の 1/3 を消化したことになります。単純計算では、このシリーズは全体で約20話分ということになります。なんだか、大リーグの大谷選手の「今期ホームラン60本ペース」というような線形予測ですね。さて、この行く末はどうなるでしょうか?
小学3年生で登場するアイテム
小学2年生までで登場したアイテムを列挙してみましょう。足し算(加算)、引き算(減算)、掛け算(乗算)、(一部の)図形、時間/時刻 です。計算としてまだ登場していないものは「割り算(除算)」ということになります。小学3年生では、この「割り算」が登場します。
また、小学2年生までで登場した図形には「三角形と四角形(直角・頂点・辺)」と「直方体と立方体」がありました。図形では、これに加えて、円 と 球 が登場します。ここで初めて曲線(と曲面)が登場する訳です。この辺りも、深掘りすると面白い分野ですが、小学3年生では直径、半径という概念は登場しますが、その面積や円周率までは出てきませんので、この話題は先送りすることにしましょう。
「等分除」「包含除」
小学3年生では「等分除」、「包含除」という概念が登場します。この単語、実は筆者は初めて目にしました(どこかで学んで忘れてしまっただけかも知れませんが…)。
例えば……
「リンゴが12個ありました。3人で均等に分けると1人分はいくつでしょう?」
答えは「4個」ですが、これを「等分除」というそうです。
「リンゴが12個ありました。1人に3個ずつ分けるとしたら何人に配れるでしょう?」
答えは「4人」ですが、これを「包含除」というそうです。
式としては、どちらも「12 ÷ 3 = 4」で区別がないと考えられます。単位が付いているから違いが出るのでは? と思ったりもしますが、実は違います。「乗法」との関係を考えるべきです。
x × 3 = 12 の x、つまり、被乗数 を求める演算が「等分除」。
3 × x = 12 の x、つまり、乗数 を求める演算が「包含除」ということになります。
整数の乗法に関しては「交換則(可換則)」が成立するので、どちらを求めても同じ結果になりますが、交換則が成立しない(可換ではない)場合には、この2つの結果は異なることになるわけです。
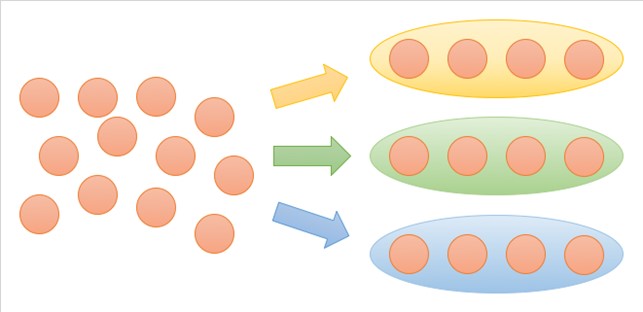
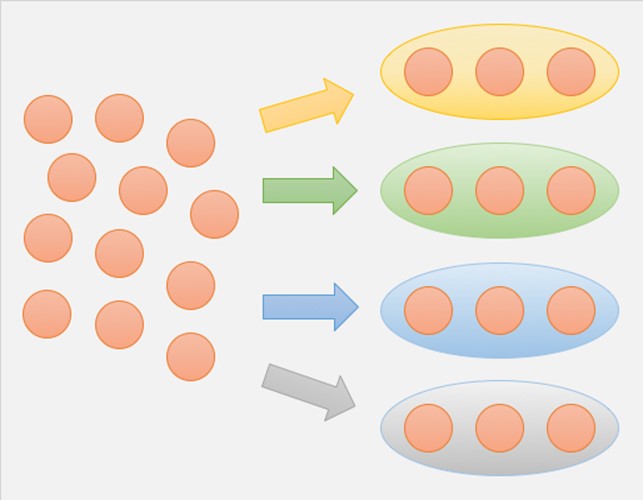
前回(第28話)でも「単位」「単位系」を話題にしましたが、「等分除」「包含除」も「単位」を意識して捉える必要があります。
等分除は「単位(単位あたりの量)を求める計算」、包含除は「単位(単位あたりの量)を使う計算」という位置付けになります。
SI基本単位でもある「モル (mol)」を考えてみましょう。モルは物質量を表す単位です。アボガドロ数 ≒ 6.02 x 10^23 個 の原子あるいは分子が集まった物質量が 1 mol です。
化学での「モル濃度」は「溶液単位体積あたりの物質量」で考えてみましょう。溶液 3L あたり溶質 12mol を含む溶液のモル濃度は 4 mol/L ということになります。溶液 300mL あたり溶質 1.2mol を含む溶液のモル濃度は 4 mol/L ということになります。これは「等分除」です。
「モル質量」は「物質量 1mol のその物質の質量」です。モル質量 12g/mol の物質 3g の モル数 は 4mol ということになります。これが「包含除」です。
小学3年生の課程では「モル」も「モル濃度」「モル質量」も登場しません。しかし、割り算(除算)には2つの位置付けがあるということを感覚的で良いので把握して欲しい、という含意が指導要綱にあるのだろうと思います。
まとめ
小学3年生に進級したばかりで「単位」というモノを改めて考えさせられるテーマが登場しました。算数は、数学は、単位を含めあらゆる物事の土台だということを感じて頂ければ幸甚です。次回は記念すべき「第30話」です。引き続き、小学3年生の題材を学びましょう。小学3年生では「剰余」「小数」「分数」という重要な概念が登場します。
四方山話
モルは「物質量」ですが、長さでもなく、質量でもなく、時間でもなく、電流でもなく、温度でもなく、光度でもなく、ある意味では単なる「数」です。単なる「数」は時に「無次元量」「無次元数」と呼ばれたりもします。
長さを長さで割ったモノ、例えば(タイヤの扁平率などを表す)アスペクトレシオの「次元」は「m⁄m」です。
力学に登場する「反発係数 e」は、速度を速度で割ったモノ「 ㎳-1/㎳-1」です。 流体力学に登場する「レイノズル数 Re」は、流体の速度と移動距離の積を動粘性係数で割ったモノ「ms-1×m/m2s-1」です。自分も安易に「無次元数」と言ってしまうことがありますが、モル、アスペクトレシオ、反発係数、レイノズル数は、当然ながら表しているものが異なります。単位が異なるということです。「無次元数」と括ってしまって、同じ「単位」と扱えるものではない。「等分除」「包含除」についての話を友人としていて、安易に「無次元」を使ってはいけないことに気付かされました。
CS四方山話の過去の記事はこちら(合わせてお読みください)

中村 健 (Ken Nakamura)
株式会社SYNCHRO 取締役 CTO
機械屋だったはずだが、いつの間にかソフト屋になっていた。
以前は計測制御、知識工学が専門分野で、日本版スペースシャトルの飛行実験に関わったり、アクアラインを掘ったりしていた。
VoIPに関わったことで通信も専門分野に加わり、最近はネットワークセキュリティに注力している。
https://www.udc-synchro.co.jp/
サイバーセキュリティ四方山話の最新話は、メールマガジンにてもご案内致しています。是非JAPANSecuritySummit Updateのメールマガジンにご登録ください。
メールマガジンの登録はこちらからお願いします。